
【题目】如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D. 
(1)求证:CE2=CDCB.
(2)若AB=2,BC= ![]() ,求CE与CD的长.
,求CE与CD的长.
【答案】
(1)证明:如图示:

连接BE,
∵BC为⊙O的切线∴∠ABC=90°,
∵AB为⊙O的直径∴∠AEB=90°,
∴∠DBE+∠OBE=90°,∠AEO+∠OEB=90°,
∵OB=OE,∴∠OBE=∠OEB∴∠DBE=∠AEO,
∵∠AEO=∠CED∴∠CED=∠CBE,
∵∠C=∠C∴△CED∽△CBE,
∴ ![]() =
= ![]() ,∴CE2=CDCB;
,∴CE2=CDCB;
(2)解:∵OB=1,BC= ![]() ,∴OC=
,∴OC= ![]() ,
,
∴CE=OC﹣OE= ![]() ,
,
由(Ⅰ)得:CE2=CDCB,
∴ ![]() =
= ![]() CD,
CD,
∴CD= ![]() .
.
【解析】(1)要证CE2=CDCB,结合题意,只需证明△CED∽△CBE即可,故连接BE,利用弦切角的知识即可得证;(2)在Rt三△OBC中,利用勾股定理即可得出CE的长,由(1)知,CE2=CDCB,代入CE即可得出CD的长.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程为ρ=2cosθ,θ∈[0, ![]() ]
]
(1)求C的参数方程;
(2)设点D在半圆C上,半圆C在D处的切线与直线l:y= ![]() x+2垂直,根据(1)中你得到的参数方程,求直线CD的倾斜角及D的坐标.
x+2垂直,根据(1)中你得到的参数方程,求直线CD的倾斜角及D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对![]() 名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝
名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝![]() 以上为“常喝”,体重超过
以上为“常喝”,体重超过![]() 为“肥胖”.
为“肥胖”.
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到肥胖的学生的概率为
人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中恰有2名女生,现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目,求恰好抽到一名男生和一名女生的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体ABCD中,过棱AB的上一点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H

(1)求证:截面EFGH为平行四边形
(2)若P、Q在线段BD、AC上,![]() ,且P、F不重合,证明:PQ∥截面EFGH
,且P、F不重合,证明:PQ∥截面EFGH
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.
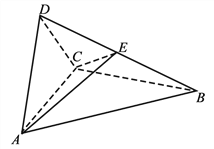
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的偶函数f(x)满足对x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,则a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标系xOy平面内,已知动点M到点D(﹣4,0)与E(﹣1,0)的距离之比为2.
(1)求动点M的轨迹C的方程;
(2)是否存在经过点(﹣1,1)的直线l,它与曲线C相交于A,B两个不同点,且满足 ![]() (O为坐标原点)关系的点M也在曲线C上,如果存在,求出直线l的方程;如果不存在,请说明理由.
(O为坐标原点)关系的点M也在曲线C上,如果存在,求出直线l的方程;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com