
分析 (1)|f(x)|=|a|log2x|+1|,∴F(x)≠|f(x)|;①不对:(2)F(-x)=F(x),函数F(x)是偶函数;故②正确
(3)|log2m|>|log2n|,a|log2m|+1>a|log2n|+1,即F(m)<F(n)成立;故F(m)-F(n)<0成立;所以③正确
(4)x>0时,F(x)的最小值为F(1)=1,运用图象判断即可.
解答 解:解:(1)∵函数f(x)=a|log2x|+1(a≠0),定义函数F(x)=$\left\{\begin{array}{l}{f(x),x>0}\\{f(-x),x<0}\end{array}\right.$,
对于①,∴|f(x)|=|a|log2x|+1|,∴F(x)≠|f(x)|;故①不错;
对于②,F(x)=$\left\{\begin{array}{l}{f(x),x>0}\\{f(-x),x<0}\end{array}\right.$═F(x)∴函数F(x)是偶函数;故②正确,
对于③,∵当a<0时,若0<m<n<1,∴|log2m|>|log2n|
∴a|log2m|+1>a|log2n|+1,即F(m)<F(n)成立;故F(m)-F(n)<0成立;所以③正确;
对于④,∴x>0时,F(x)在(0,1)单调递减,(1,+∞)单调递增,∴x>0时,F(x)的最小值为F(1)=1,
故x>0时,F(x)与y=-2有2个交点,∵函数F(x)是偶函数,∴x<0时,F(x)与y=-2有2个交点
故当a>0时,函数y=F(x)-2有4个零点.所以④正确,
故答案为:②③④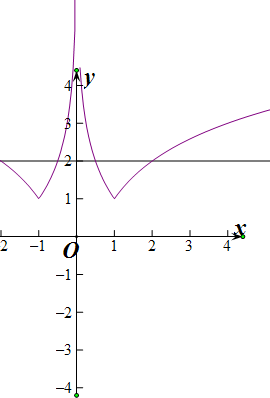
点评 本题综合考察了函数的性质,运用图象解决问题,对于函数式子与性质的结合,关键是理解,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 截两坐标轴所得弦的长度相等 | B. | 与两坐标轴都相切 | ||
| C. | 与两坐标轴相离 | D. | 上述情况都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a>b>c | C. | c>a>b | D. | a<c<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com