
【题目】已知函数![]() ,
,![]() ,直线
,直线![]() 与曲线
与曲线![]() 切于点
切于点![]() ,且与曲线
,且与曲线![]() 切于点
切于点![]() .
.
(1)求实数![]() 的值;
的值;
(2)证明:(ⅰ)![]() ;(ⅱ)当
;(ⅱ)当![]() 为正整数时,
为正整数时,![]()
【答案】(1)![]() ,(2)证明见解析
,(2)证明见解析
【解析】
试题分析:(Ⅰ)先求出![]() ,
,![]() ,再利用导数的几何意义求出切线方程,进而得到
,再利用导数的几何意义求出切线方程,进而得到![]() . (Ⅱ)证明:(ⅰ)由于
. (Ⅱ)证明:(ⅰ)由于![]() ,由题意可构造函数
,由题意可构造函数![]() ,
,
再求![]() ,得到函数
,得到函数![]() 的单调性,可得
的单调性,可得![]() ;同理再构造函数
;同理再构造函数![]() ,得到
,得到![]() ,从而不等式
,从而不等式![]() 成立.
成立.
(ⅱ)证明本题时,注意(ⅰ)的结论的应用,取![]() 得:
得:![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,作差
时,作差![]() 比较
比较![]() 的大小,可证出
的大小,可证出![]() .
.
又![]() ,
,
故![]() ,利用放缩法得到
,利用放缩法得到![]() 证毕
证毕
试题解析:(Ⅰ)由![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,
,
曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,即
,即![]() ,
,
依题意,得![]() .
.
(Ⅱ)证明:(ⅰ)![]() ,令
,令![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 单调递减,
单调递减,
所以![]() ;
;
令![]() ,则
,则![]()
所以![]() 单调递减,故
单调递减,故![]() ,
,
所以![]() 成立.
成立.
(ⅱ)由(ⅰ),取![]() 得:
得:![]() ,
,
令![]() ,
,
则![]() ,当
,当![]() 时,
时,
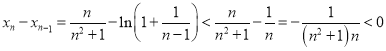 .
.
因此![]() .
.
又![]() ,
,
故![]()
 ,
,
所以当![]() 为正整数时,
为正整数时,![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】我国是水资源匮乏的国家,为鼓励节约用水,某市打算出台一项水费政策措施.规定:每季度每人用水量不超过5吨时,每吨水费收基本价1.3元;若超过5吨而不超过6吨时,超过部分的水费按基本价3倍收取;若超过6吨而不超过7吨时,超过部分的水费按基本价5倍收取.某人本季度实际用水量为![]()
![]() 吨,应交水费为
吨,应交水费为![]() 元.
元.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)试求出函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列抽样问题中,最适合用系统抽样的是( )
A.从全班48名学生中随机抽取8人参加一项活动
B.一个城市有210家百货商店,其中有大型商店20家,中型商店40家,小型商店150家,为了掌握各商店的营业情况,要从中抽取一个容量为21的样本
C.从参加考试的1200名考生中随机抽取100人分析试题作答情况
D.从参加模拟考试的1200名高中生中随机抽取10人了解情况
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如(1)图所示,在直角梯形ABCD中,AD∥BC,![]() ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
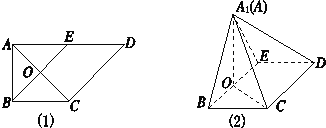
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编为1~50号,并进行分组,第一组1~5号,第二组6~10号,…,第十组46~50号.若在第三组中抽得号码为12的学生,则在第九组中抽得号码为_____的学生.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于直线的倾斜角与斜率,下列说法正确的是( )
A.所有的直线都有倾斜角和斜率
B.所有的直线都有倾斜角但不一定都有斜率
C.直线的倾斜角和斜率有时都不存在
D.所有的直线都有斜率,但不一定有倾斜角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com