Question

【题目】已知空间几何体ABCDE中，△BCD与△CDE均是边长为2的等边三角形，△ABC是腰长为3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD.

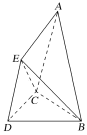
(1)试在平面BCD内作一条直线，使得直线上任意一点F与E的连线EF均与平面ABC平行，并给出证明；

(2)求三棱锥E－ABC的体积.

Answer 1

【答案】（1）取DC的中点N，取BD的中点M，连接MN，则MN即为所求，证明见解析（2）

【解析】

（1）取DC的中点N，取BD的中点M，连接MN，则MN即为所求，证明EN∥AH，MN∥BC可得平面EMN∥平面ABC即可（2）因为点E到平面ABC的距离与点N到平面ABC的距离相等，求三棱锥E－ABC的体积可转化为求三棱锥N－ABC的体积，根据体积公式计算即可.

(1)如图所示，取DC的中点N，取BD的中点M，连接MN，则MN即为所求.

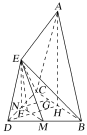
证明：连接EM，EN，取BC的中点H，连接AH，

∵△ABC是腰长为3的等腰三角形，H为BC的中点，

∴AH⊥BC，又平面ABC⊥平面BCD，平面ABC∩平面BCD＝BC，AH平面ABC，

∴AH⊥平面BCD，同理可证EN⊥平面BCD，

∴EN∥AH，

∵EN平面ABC，AH平面ABC，

∴EN∥平面ABC.

又M，N分别为BD，DC的中点，

∴MN∥BC，

∵MN平面ABC，BC平面ABC，

∴MN∥平面ABC.

又MN∩EN＝N，MN平面EMN，EN平面EMN，

∴平面EMN∥平面ABC，

又EF平面EMN，

∴EF∥平面ABC，

即直线MN上任意一点F与E的连线EF均与平面ABC平行.

(2)连接DH，取CH的中点G，连接NG，则NG∥DH，

由(1)可知EN∥平面ABC，

∴点E到平面ABC的距离与点N到平面ABC的距离相等，

又△BCD是边长为2的等边三角形，

∴DH⊥BC，

又平面ABC⊥平面BCD，平面ABC∩平面BCD＝BC，DH平面BCD，

∴DH⊥平面ABC，∴NG⊥平面ABC，

易知DH＝，∴NG＝，

又S△ABC＝·BC·AH＝×2×＝2，

∴VE－ABC＝·S△ABC·NG＝.