
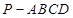 中,底面
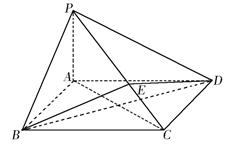
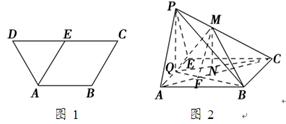
中,底面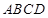 为矩形,
为矩形,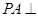 平面
平面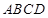 ,点
,点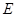 在线段
在线段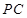 上,
上,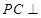 平面
平面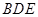 .
.
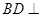 平面
平面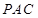 .;
.;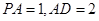 ,求三棱锥
,求三棱锥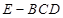 的体积.
的体积.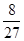
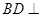 平面
平面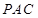 ,需证
,需证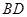 与平面
与平面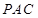 内的两条相交直线都垂直,
内的两条相交直线都垂直,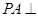 平面
平面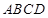 ,可证
,可证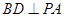 ,由
,由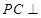 平面
平面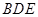 ,可证
,可证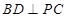 .根据线面垂直的判定定理,
.根据线面垂直的判定定理,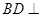 平面
平面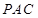 .(2)设矩形
.(2)设矩形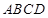 的对角线的交点为
的对角线的交点为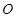 ,连结
,连结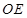 ,由(1)的结论可知
,由(1)的结论可知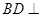 平面
平面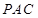 ,从而有
,从而有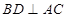 ,所以矩形
,所以矩形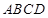 为正方形,边长为2;由
为正方形,边长为2;由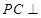 平面
平面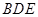 ,知
,知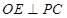 ,因此
,因此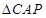 与
与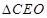 相似,可确定
相似,可确定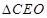 的各边长,然后由
的各边长,然后由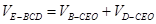 求三棱锥
求三棱锥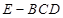 的体积.
的体积.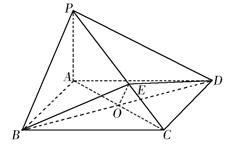
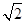 ,OC=
,OC=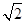 .
.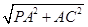 =
= =3.
=3.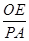 =
=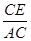 =
=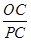 ,即
,即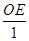 =
=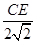 =
=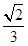 ,∴OE=
,∴OE=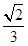 ,CE=
,CE=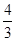 .
.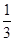 S△CEO·BD=
S△CEO·BD=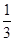 ·
·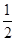 OE·CE·BD=
OE·CE·BD=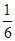 ·
·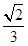 ·
·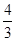 ·2
·2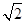 =
=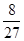 . 13分
. 13分

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com