
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 为椭圆上一动点,当
为椭圆上一动点,当![]() 的面积最大时,其内切圆半径为
的面积最大时,其内切圆半径为![]() ,设过点
,设过点![]() 的直线
的直线![]() 被椭圆
被椭圆![]() 截得线段
截得线段![]() ,
,
当![]() 轴时,
轴时,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 为椭圆
为椭圆![]() 的左顶点,
的左顶点,![]() 是椭圆上异于左、右顶点的两点,设直线
是椭圆上异于左、右顶点的两点,设直线![]() 的斜率分别为
的斜率分别为![]() ,若
,若![]() ,试问直线
,试问直线![]() 是否过定点?若过定点,求该定点的坐标;若不过定点,请说明理由.
是否过定点?若过定点,求该定点的坐标;若不过定点,请说明理由.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 过定点,定点坐标为
过定点,定点坐标为![]() .
.
【解析】
(1)根据三角形内切圆的性质得到![]() 的关系,结合已知条件,可求椭圆方程。
的关系,结合已知条件,可求椭圆方程。
(2)在(1)的条件下,当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,代入椭圆方程,运用韦达定理和直线的斜率公式,化简整理,再由直线恒过定点的求法,即可得到所求定点,切记在斜率不存在时进行检验。
,代入椭圆方程,运用韦达定理和直线的斜率公式,化简整理,再由直线恒过定点的求法,即可得到所求定点,切记在斜率不存在时进行检验。
解:(1)由题意及三角形内切圆的性质可得![]() ,得
,得![]() ①
①
将![]() 代入
代入![]() ,结合
,结合![]() ②,得
②,得![]() ,
,
所以![]() ③,由①②③得
③,由①②③得![]()
故椭圆![]() 的标准方程为
的标准方程为![]()
(2)设点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
①当直线![]() 的斜率不存在时,由题意得
的斜率不存在时,由题意得![]() 或
或![]() ,
,
直线![]() 的方程为
的方程为![]()
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
联立得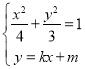 ,消去
,消去![]() 得
得![]() ,
,
由![]() ,得
,得![]()
![]() )
)
由![]() 可得
可得![]() ,
,
得![]() ,
,
整理得![]()
由(1)和(2)得![]() ,解得
,解得![]() 或
或![]()
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,过定点
,过定点![]() ,不合题意;
,不合题意;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,过定点
,过定点![]() ,
,
综上直线![]() 过定点,定点坐标为
过定点,定点坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数g(x)=-2x+3.
,函数g(x)=-2x+3.
(1)当a=2时,求f(x)的极值;
(2)讨论函数![]() 的单调性;
的单调性;
(3)若-2≤a≤-1,对任意x1,x2∈[1,2],不等式|f(x1)-f(x2)|≤t|g(x1)-g(x2)|恒成立,求实数t的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专章规定.草案提出,国家推行生活垃圾分类制度.为了了解人民群众对垃圾分类的认识,某市环保部门对该市市民进行了一次垃圾分类网络知识问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
得分 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,市环保部门为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设满足以下两个条件的有穷数列![]() 为
为![]() 阶“期待数列”:①
阶“期待数列”:①![]() ;②
;②![]() .
.
(1)分别写出一个单调递增的3阶和4阶“期待数列”;
(2)若某2013阶“期待数列”是等差数列,求该数列的通项公式;
(3)记![]() 阶“期待数列”的前
阶“期待数列”的前![]() 项和为
项和为![]() ,试证:
,试证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差不为0的等差数列,
是公差不为0的等差数列,![]() ,数列
,数列![]() 是等比数列,且
是等比数列,且![]() ,
,![]() ,
,![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设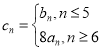 ,求
,求![]() 的前n项和
的前n项和![]() ;
;
(3)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在一山坡![]() 处看对面山顶上的一座铁塔,如图所示,塔及所在的山崖可视为图中的竖线
处看对面山顶上的一座铁塔,如图所示,塔及所在的山崖可视为图中的竖线![]() ,塔高
,塔高![]() 为80米,山高
为80米,山高![]() 为220米,
为220米,![]() 为200米,图中所示的山坡可视为直线
为200米,图中所示的山坡可视为直线![]() 且点
且点![]() 在直线
在直线![]() 上,
上,![]() 与水平地面的夹角为
与水平地面的夹角为![]() ,
,![]() .
.

(1)求塔尖![]() 到山坡的距离;(精确到米)
到山坡的距离;(精确到米)
(2)问此同学(忽略身高)距离山崖的水平地面多高时,观看塔的视角![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com