
分析 (Ⅰ)由椭圆离心率可得a,c的关系,结合|PF1|•|PF2|的最大值是2求得a,再由隐含条件求得b,则椭圆方程可求;
(Ⅱ)设A(x1,y1),B(x2,y2),则设直线l的方程为x=my+n,由直线与圆x2+y2=1只有一个交点,得n2=m2+1,把x=my+n代入椭圆方程,可得$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=(1+m2)y1y2+mn(y1+y2)+n2=$\frac{{m}^{2}+1}{{m}^{2}+2}$,把S△AOB化为含有$\frac{{m}^{2}+1}{{m}^{2}+2}$的式子,结合$\frac{2}{3}$≤$\overrightarrow{OA}$•$\overrightarrow{OB}$≤$\frac{3}{4}$求△AOB面积S的取值范围,则最大值可求.
解答 解:(Ⅰ)由$e=\frac{c}{a}=\frac{\sqrt{2}}{2}$,得a=$\sqrt{2}c$,
由|PF1|•|PF2|≤$(\frac{|P{F}_{1}|+|P{F}_{2}|}{2})^{2}$=$\frac{4{a}^{2}}{4}={a}^{2}$,且|PF1|•|PF2|的最大值是2,得a2=2,
∴a=$\sqrt{2}$,则c=1,
∴b2=a2-c2=1,
则椭圆C1的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(Ⅱ)圆x2+y2=b2=1.
依题知l的斜率不可能为零,设直线l的方程为x=my+n(m∈R).
∵直线x-my-n=0与圆x2+y2=1只有一个交点,
∴有:$\frac{|n|}{\sqrt{{m}^{2}+1}}=1$,得n2=m2+1.
设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{x=my+n}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,消去x整理得:(m2+2)y2+2mny+n2-2=0,
则y1+y2=-$\frac{2mn}{{m}^{2}+2}$,y1y2=$\frac{{n}^{2}-2}{{m}^{2}+2}$.
其判别式△=8(m2-n2+2)=8,
∵$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=(1+m2)y1y2+mn(y1+y2)+n2=$\frac{{m}^{2}+1}{{m}^{2}+2}$.
∴S△AOB=$\frac{1}{2}$|$\overrightarrow{OA}$||$\overrightarrow{OB}$|sin∠AOB=$\frac{1}{2}$|x1y2-x2y1|=$\frac{1}{2}$|n(y2-y1)|=$\frac{1}{2}$|n|×$\frac{\sqrt{△}}{{m}^{2}+2}$
=$\sqrt{2}$•$\sqrt{\frac{{m}^{2}+1}{{m}^{2}+2}•\frac{1}{{m}^{2}+2}}$=$\sqrt{2}$•$\sqrt{\frac{{m}^{2}+1}{{m}^{2}+2}•(1-\frac{{m}^{2}+1}{{m}^{2}+2})}$,
令t=$\frac{{m}^{2}+1}{{m}^{2}+2}$,则由$\frac{2}{3}$≤$\overrightarrow{OA}$•$\overrightarrow{OB}$≤$\frac{3}{4}$,知$\frac{2}{3}$≤t≤$\frac{3}{4}$,
∴$\frac{\sqrt{6}}{4}$≤S△AOB≤$\frac{2}{3}$.
∴△AOB面积S的最大值为$\frac{2}{3}$.
点评 本题考查圆锥曲线的性质和综合应用,解题时要注意向量的数量积公式、点到直线的距离公式的灵活运用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
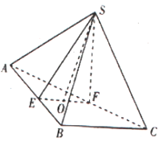 如图,三棱锥S-ABC,E,F分别在线段AB,AC上,EF∥BC,△ABC,△SEF均是等边三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O为EF的中点.
如图,三棱锥S-ABC,E,F分别在线段AB,AC上,EF∥BC,△ABC,△SEF均是等边三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O为EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com