
【题目】已知抛物线![]() 的焦点
的焦点![]() ,
,![]() 上一点坐标为
上一点坐标为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过![]() 作直线
作直线![]() ,交抛物线
,交抛物线![]() 于
于![]() ,
,![]() 两点,若直线
两点,若直线![]() 中点的纵坐标为
中点的纵坐标为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将点坐标代入解析式,求得![]() 的值,即可求得抛物线方程.
的值,即可求得抛物线方程.
(2)方法一:设点![]() ,
,![]() ,根据中点纵坐标即可利用点差法求得直线的斜率,由点斜式即可求得直线方程;方法二,设出直线方程,联立直线方程与抛物线方程,根据韦达定理和中点的纵坐标,即可求得直线方程.
,根据中点纵坐标即可利用点差法求得直线的斜率,由点斜式即可求得直线方程;方法二,设出直线方程,联立直线方程与抛物线方程,根据韦达定理和中点的纵坐标,即可求得直线方程.
(1)把![]() 代入抛物线方程
代入抛物线方程
解得![]()
∴![]() 的方程为
的方程为![]() .
.
(2)法一:由(1)得抛物线![]() 的方程为
的方程为![]() ,焦点
,焦点![]()
设![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,代入抛物线可得
,代入抛物线可得
则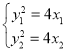 ,两式相减,整理得
,两式相减,整理得![]()
∵线段![]() 中点的纵坐标为
中点的纵坐标为![]()
∴直线![]() 的斜率
的斜率![]()
直线![]() 的方程为
的方程为![]() 即
即![]()
法二:由(1)得抛物线![]() 的方程为
的方程为![]() ,焦点
,焦点![]()
设直线![]() 的方程为
的方程为![]()
由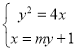 消去
消去![]() ,得
,得![]()
设![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,
,
∵线段![]() 中点的纵坐标为
中点的纵坐标为![]()
∴![]()
解得![]()
直线![]() 的方程为
的方程为![]() 即
即![]()


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】已知点P到直线y=﹣4的距离比点P到点A(0,1)的距离多3.
(1)求点P的轨迹方程;
(2)经过点Q(0,2)的动直线l与点P的轨交于M,N两点,是否存在定点R使得∠MRQ=∠NRQ?若存在,求出点R的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥
中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥![]() 的体积为
的体积为![]()
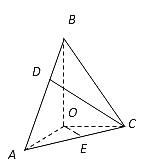
(1)求三棱锥![]() 的高;
的高;
(2)在线段AB上取一点D,当D在什么位置时,![]() 和
和![]() 的夹角大小为
的夹角大小为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,下列结论中错误的是
,下列结论中错误的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函数y=f(x)的图像是中心对称图形
C. 若![]() 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞,![]() )单调递减
)单调递减
D. 若![]() 是f(x)的极值点,则
是f(x)的极值点,则![]() (
(![]() )=0
)=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax-alnx(a∈R).
(1)若函数f(x)在x=1处取得极值,求a的值;
(2)在(1)的条件下,求证:f(x)≥-![]() +
+![]() -4x+
-4x+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到焦点的距离为4,动直线
到焦点的距离为4,动直线![]() 交抛物线
交抛物线![]() 于坐标原点O和点A,交抛物线
于坐标原点O和点A,交抛物线![]() 的准线于点B,若动点P满足
的准线于点B,若动点P满足![]() ,动点P的轨迹C的方程为
,动点P的轨迹C的方程为![]() .
.
(1)求出抛物线![]() 的标准方程;
的标准方程;
(2)求动点P的轨迹方程![]() ;
;
(3)以下给出曲线C的四个方面的性质,请你选择其中的三个方面进行研究:①对称性;②范围;③渐近线;④![]() 时,写出由
时,写出由![]() 确定的函数
确定的函数![]() 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年![]() 年月某市邮政快递业务量完成件数较2017年月
年月某市邮政快递业务量完成件数较2017年月![]() 月同比增长
月同比增长![]() ,如图为该市2017年
,如图为该市2017年![]() 月邮政快递业务量柱状图及2018年
月邮政快递业务量柱状图及2018年![]() 月邮政快递业务量饼图,根据统计图,解决下列问题
月邮政快递业务量饼图,根据统计图,解决下列问题

![]() 年
年![]() 月该市邮政快递同城业务量完成件数与2017年
月该市邮政快递同城业务量完成件数与2017年![]() 月相比是有所增大还是有所减少,并计算,2018年
月相比是有所增大还是有所减少,并计算,2018年![]() 月该市邮政快递国际及港澳台业务量同比增长率;
月该市邮政快递国际及港澳台业务量同比增长率;
![]() 若年平均每件快递的盈利如表所示:
若年平均每件快递的盈利如表所示:
快递类型 | 同城 | 异地 | 国际及港澳台 |
盈利 |
| 5 | 25 |
估计该市邮政快递在2018年![]() 月的盈利是多少?
月的盈利是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com