
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数且
为参数且 ![]() )曲线
)曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),以
),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的交点到极点的距离;
的交点到极点的距离;
(2)设![]() 与
与![]() 交于
交于![]() 点,
点,![]() 与
与![]() 交于
交于![]() 点,当
点,当![]() 在
在![]() 上变化时,求
上变化时,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】近年来,随着“一带一路”倡议的推进,中国与沿线国家旅游合作越来越密切,中国到“一带一路”沿线国家的游客人也越来越多,如图是2013-2018年中国到“一带一路”沿线国家的游客人次情况,则下列说法正确的是( )
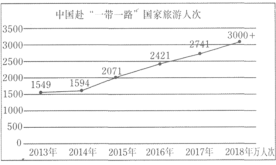
①2013-2018年中国到“一带一路”沿线国家的游客人次逐年增加
②2013-2018年这6年中,2016年中国到“一带一路”沿线国家的游客人次增幅最小
③2016-2018年这3年中,中国到“一带一路”沿线国家的游客人次每年的增幅基本持平
A.①③B.②③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() :
:![]() 截
截![]() 轴所得的线段长等于
轴所得的线段长等于![]() .
.![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 相交于点
相交于点![]() 直线
直线![]() 分别与
分别与![]() 相交于
相交于![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,
,![]() 的面积分别为
的面积分别为![]() ,若
,若![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个铝合金窗分为上、下两栏,四周框架和中间隔档的材料为铝合金,宽均为6![]() ,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800
,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800![]() ,设该铝合金窗的宽和高分别为
,设该铝合金窗的宽和高分别为![]() ,铝合金窗的透光部分的面积为
,铝合金窗的透光部分的面积为![]() .
.
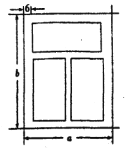
(1)试用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
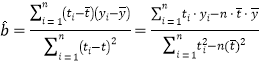 ,
,![]()
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区2019(![]() )年该农产品的产量;
)年该农产品的产量;
②当![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神舟十一号”飞船进行新产品搭载实验,计划搭载新产品![]() ,要根据该产品的研制成本、产品质量、搭载实验费用和预计产生收益来决定具体安排,通过调查,搭载每件产品有关数据如表:
,要根据该产品的研制成本、产品质量、搭载实验费用和预计产生收益来决定具体安排,通过调查,搭载每件产品有关数据如表:
因素 | 产品 | 产品 | 备注 |
研制成本、搭载费用之和/万元 | 20 | 30 | 计划最大投资 |
金额300万元产品质量/千克 | 10 | 5 | 最大搭载 |
质量110千克预计收益/万元 | 80 | 60 | —— |
则使总预计收益达到最大时, ![]() 两种产品的搭载件数分别为( )
两种产品的搭载件数分别为( )
A. 9,4 B. 8,5 C. 9,5 D. 8,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com