
【题目】已知函数![]() ,下列结论中正确的序号是__________.
,下列结论中正确的序号是__________.
①![]() 的图象关于点
的图象关于点![]() 中心对称,
中心对称,
②![]() 的图象关于
的图象关于![]() 对称,
对称,
③![]() 的最大值为
的最大值为![]() ,
,
④![]() 既是奇函数,又是周期函数.
既是奇函数,又是周期函数.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为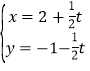 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈尔滨市第三中学校响应教育部门疫情期间“停课不停学”的号召,实施网络授课,为检验学生上网课的效果,高三学年进行了一次网络模拟考试.全学年共![]() 人,现从中抽取了
人,现从中抽取了![]() 人的数学成绩,绘制成频率分布直方图(如下图所示).已知这
人的数学成绩,绘制成频率分布直方图(如下图所示).已知这![]() 人中
人中![]() 分数段的人数比
分数段的人数比![]() 分数段的人数多
分数段的人数多![]() 人.
人.
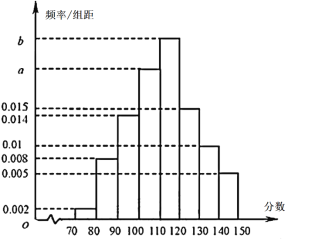
(1)根据频率分布直方图,求![]() 、
、![]() 的值,并估计抽取的
的值,并估计抽取的![]() 名同学数学成绩的中位数;
名同学数学成绩的中位数;
(2)若学年打算给数学成绩不低于![]() 分的同学颁发“网络课堂学习优秀奖”,将这
分的同学颁发“网络课堂学习优秀奖”,将这![]() 名同学数学成绩的样本频率视为概率.
名同学数学成绩的样本频率视为概率.
(i)估计全学年的获奖人数;
(ii)若从全学年随机选取![]() 人,求所选
人,求所选![]() 人中至少有
人中至少有![]() 人获奖的概率.
人获奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为改善环境,节约资源,我国自2019年起在全国地级及以上城市全面启动生活垃圾分类,垃圾分类已成为一种潮流.某市一小区的主管部门为了解居民对垃圾分类的认知是否与其受教育程度有关,对该小区居民进行了随机抽样调查,得到如下统计数据的列联表:
知道如何对垃圾进行分类 | 不知道如何对垃圾进行分类 | 合计 | |
未受过高等教育 |
| 10 |
|
受过高等教育 |
|
|
|
合计 |
|
| 50 |
(1)求列联表中的![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值,并估计该小区受过高等教育的居民知道如何对垃圾进行分类的概率;
的值,并估计该小区受过高等教育的居民知道如何对垃圾进行分类的概率;
(2)根据列联表判断能否有![]() 的把握认为该小区居民对垃圾分类的认知与其受教育程度有关?
的把握认为该小区居民对垃圾分类的认知与其受教育程度有关?
参考数据及公式:
|
|
|
|
|
|
|
|
|
|
|
|
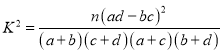 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900
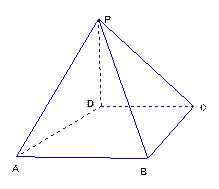
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a=2![]() ,_______,求△ABC的周长l的范围.
,_______,求△ABC的周长l的范围.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:这三个条件中任选一个,补充在上面问题中并对其进行求解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=lnx,g(x)=ex.
(1)若函数φ (x) = f (x)-![]() ,求函数φ (x)的单调增区间;
,求函数φ (x)的单调增区间;
(2)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com