
分析 (1)由已知及倍角公式可求cosA,sinA,又$\overrightarrow{AB}•\overrightarrow{AC}=3$,得bccosA=3,解得bc=5,利用三角形面积公式即可得解.
(2)利用余弦定理可得a2=b2+c2-6,利用基本不等式即可得解.
解答 解:(1)因为:$cos\frac{A}{2}=\frac{{2\sqrt{5}}}{5}$,
所以:$cosA=2{cos^2}\frac{A}{2}-1=\frac{3}{5}$,(2分)
可得:$sinA=\frac{4}{5}$,(3分)
又因为:$\overrightarrow{AB}•\overrightarrow{AC}=3$,得bccosA=3,(4分)
可得:bccosA=3⇒bc=5,(5分)
$⇒{S_{△ABC}}=\frac{1}{2}bcsinA=2$.(7分)
(2)∵bc=5,
∴${a^2}={b^2}+{c^2}-2bccosA={b^2}+{c^2}-2×5×\frac{3}{5}$,(10分)
∴a2=b2+c2-6,(11分)
$\begin{array}{l}∴\;\;\;\;\;{a^2}={b^2}+{c^2}-6⇒{b^2}+{c^2}=6+{a^2}≥2bc=10\\∴\;\;\;\;\;\;\;{a_{min}}=2\end{array}$(12分)
当且仅当b=c=$\sqrt{5}$时a最小值是2.(14分)
点评 本题主要考查了倍角公式,平面向量数量积的运算,考查了三角形面积公式,余弦定理,基本不等式的综合应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
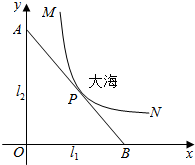 某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
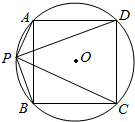 已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.
已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com