
【题目】对于定义域相同的函数![]() 和
和![]() ,若存在实数
,若存在实数![]() ,
,![]() 使
使![]() ,则称函数
,则称函数![]() 是由“基函数
是由“基函数![]() ,
,![]() ”生成的.
”生成的.
(1)若函数![]() 是“基函数
是“基函数![]() ,
,![]() ”生成的,求实数
”生成的,求实数![]() 的值;
的值;
(2)试利用“基函数![]() ,
,![]() ”生成一个函数
”生成一个函数![]() ,且同时满足:①
,且同时满足:①![]() 是偶函数;②
是偶函数;②![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .求函数
.求函数![]() 的解析式.
的解析式.
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1 , l2分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明AR∥FQ;
(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E,F分别是AB,PD的中点,若PA=AD=3,CD=![]()
①求证:AF∥平面PCE
②求证:平面PCE⊥平面PCD
③求直线FC与平面PCE所成角的正弦值.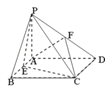
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(8)的值;
(2)求不等式f(x)-f(x-2)>3的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.![]() 年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本
年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本![]() 万元,每生产
万元,每生产![]() (百辆),需另投入成本
(百辆),需另投入成本![]() 万元,且
万元,且 .由市场调研知,每辆车售价
.由市场调研知,每辆车售价![]() 万元,且全年内生产的车辆当年能全部销售完.
万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (百辆)的函数关系式;(利润=销售额-成本)
(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com