练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．设实数a，b满足2a+b=9．
    （1）若|9-b|+|a|＜3，求a的取值范围；
    （2）求|3a-b|+|a-2b|的最小值．

    分析 （1）由条件可得3|a|＜3，利用绝对值不等式的解法，求得a的范围．
    （2）要求的式子即|5a-9|+|5a-18|，再利用绝对值三角不等式求得它的最小值．

    解答 解：实数a，b满足2a+b=9．
    （1）∵|9-b|+|a|=|2a|+|a|=3|a|＜3，∴|a|＜1，∴-1＜a＜1，故要求的a的取值范围为（-1，1）．
    （2）求|3a-b|+|a-2b|=|3a-（9-2a）|+|a-2（9-2a）|=|5a-9|+|5a-18|≥|（5a-9）-（5a-18）|=9，
    故|3a-b|+|a-2b|的最小值为9．

    点评 本题主要考查绝对值不等式的解法，绝对值三角不等式的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．设f（x）=2x+3x-8，则方程f（x）=0的根落在区间（　　）
    A．（0，1）B．（1，2）C．（2，3）D．（3，4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．抛物线y2=2px的准线方程是x=-2，则p的值是（　　）
    A．$-\frac{1}{8}$B．$\frac{1}{8}$C．-4D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．若双曲线C与椭圆x2+4y2=64有相同的焦点，它的一条渐近线方程是$x+\sqrt{3}y=0$，求双曲线C的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知x∈R，符号[x]表示不超过x的最大整数，若函数f（x）=$\frac{[x]}{x}$（x＞0），则给出以下四个结论正确的是（　　）
    A．函数f（x）的值域为（0，1]
    B．函数f（x）没有零点
    C．函数f（x）是（0，+∞）上的减函数
    D．函数g（x）=f（x）-a有且仅有3个零点时$\frac{3}{4}$＜a≤$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．为了检测某种产品的质量，抽取了一个容量为100的样本，数据的分组数如下：
    [10.75，10.85）3；[10.85，10.95）9；[10.95，11.05）13；
    [11.05，11.15）16；[11.15，11.25）26；[11.25，11.35）20；
    [11.35，11.45）7；[11.45，11.55）4；[11.55，11.65）2；
    估计数据落在[10.95，11.35）范围内的频率为（　　）
    A．.035B．0.5C．0.75D．0.95

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

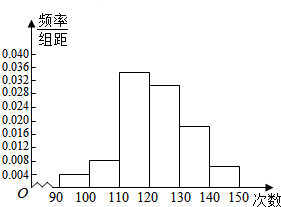    19．为了了解高一年级学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图所示），图中从左到右各小长方形的面积之比为2：4：17：15：9：3，第二小组的频数为12．则 样本容量为150．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．设数列{an}的前n项和为Sn，且满足Sn=2an-1（n∈N*）．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）求数列$\left\{{\frac{2n-1}{a_n}}\right\}$的前n项和Tn；
    （Ⅲ）数列{bn}满足bn+1=an+bn（n∈N*），且b1=3．若不等式${log_2}（{b_n}-2）＜\frac{3}{16}{n^2}+t$对任意n∈N*恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

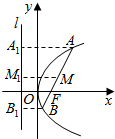    17．如图：AB是抛物线y2=2px（p＞0）过焦点F的一条弦，设A（x1，y1），B（x2，y2），AB的中点M（x0，y0），相应的准线为l．
    证明：
    （1）以AB为直径的圆必与准线l相切；
    （2）|AB|=2（x0+$\frac{p}{2}$）（焦点弦长与中点关系）；
    （3）|AB|=x1+x2+p；
    （4）x1•x2=$\frac{{p}^{2}}{4}$，y1•y2=-p2．

    查看答案和解析>>

    同步练习册答案