
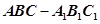 中,AB=BC,
中,AB=BC,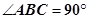 ,Q是AC上的点,AB1//平面BC1Q.
,Q是AC上的点,AB1//平面BC1Q.
 ,求二面角Q-BC1—C的余弦值.
,求二面角Q-BC1—C的余弦值. .
. ,2),然后利用向量的夹角公式计算二面角Q-BC1-C的余弦值.
,2),然后利用向量的夹角公式计算二面角Q-BC1-C的余弦值.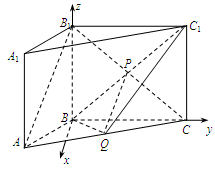
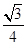 a,
a, a,0),
a,0),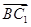 =(0,a,b),
=(0,a,b),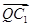 =(-
=(-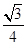 a,
a,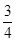 a,b).
a,b). ,
,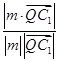 =
=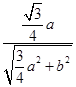 =
= ,解得b=
,解得b=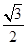 a.
a.
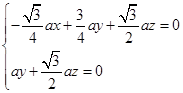 取n=(1,-
取n=(1,- ,2).
,2).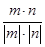 =
= .
. .
.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源:不详 题型:解答题

 的正切值.
的正切值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
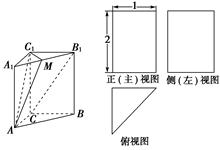
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
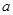 .
.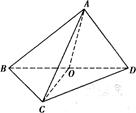
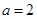 时,求证:AO⊥平面BCD;
时,求证:AO⊥平面BCD;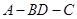 的大小为
的大小为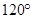 时,求二面角
时,求二面角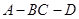 的正切值.
的正切值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com