
���� ��1����$\overrightarrow{a}$��$\overrightarrow{b}$���ɵ�$\overrightarrow{a}$•$\overrightarrow{b}$=0���������껯���������ù켣E�ķ���mx2+y2=1����Ϊ��Ԫ�������ߣ��ɷ�m=0��m=1��m��0��m��1��m��0����������ۣ�
��2����m=$\frac{1}{4}$ʱ���켣E�ķ���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}$=1����ʾ��Բ����Բ�ķ���Ϊx2+y2=r2��0��r��1����������б�ʴ���ʱ������Բ����һ���߷���Ϊy=kx+t����ֱ�ߺ�Բ���пɵ�k��t�Ĺ�ϵ����OA��OB������x1x2+y1y1=0��ֻ������ֱ�ߺ�Բ�ķ��̣���Ԫ��ά�ﶨ�����ֿ��Եõ�k��t�Ĺ�ϵ�������Ϳɽ��r��������б�ʲ�����ʱ��������鼴�ɣ���������Ӱ��������֤�����ۣ�
��� �⣺��1����Ϊ$\overrightarrow{a}$��$\overrightarrow{b}$��
����$\overrightarrow{a}$•$\overrightarrow{b}$=0������mx��y+1��•��x��y-1��=0��
��mx2+y2-1=0����mx2+y2=1��
��m=0ʱ���÷��̱�ʾ����ֱ�ߣ�
��m=1ʱ���÷��̱�ʾԲ��
��m��0��m��1ʱ���÷��̱�ʾ��Բ��
��m��0ʱ���÷��̱�ʾ˫���ߣ�
����m=$\frac{1}{4}$ʱ���켣E�ķ���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}$=1��
��Բ����ԭ���Բ��ʹ�ø�Բ������һ��������켣E������������A��B��Բ�ķ���Ϊx2+y2=r2��0��r��1����
������б�ʴ���ʱ������Բ����һ���߷���Ϊy=kx+t��
A��x1��y1����B��x2��y2����
����$\frac{|t|}{\sqrt{1+{k}^{2}}}$=r��
��t2=r2��1+k2������
��ΪOA��OB������x1x2+y1y1=0��
��x1x2+��kx1+t����kx2+t��=0��
�����ã�1+k2��x1x2+kt��x1+x2��+t2=0����
�ɷ�����$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=+tkx}\end{array}\right.$
��ȥy�ã�1+4k2��x2+8ktx+4t2-4=0����
��Τ�ﶨ��x1+x2=-$\frac{8kt}{1+4{k}^{2}}$��x1x2=$\frac{4{t}^{2}-4}{1+4{k}^{2}}$
�����ʽ��������
��1+k2��$\frac{4{t}^{2}-4}{1+4{k}^{2}}$-kt•$\frac{8kt}{1+4{k}^{2}}$+t2=0��
��5t2=4+4k2��
��Ϣ�ʽ��5r2=4��r=$\frac{2\sqrt{5}}{5}$�ʣ�0��1����
������б�ʲ�����ʱ��x2+y2=$\frac{4}{5}$Ҳ�������⣬
������Բ�ķ���Ϊx2+y2=$\frac{4}{5}$��
����$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$=$\frac{1}{AC•AB}$+$\frac{1}{BC•AB}$=$\frac{1}{AC•BC}$=$\frac{5}{4}$��
���� ���⿼����켣���̡�����������ʾ�����ߡ�ֱ����Բ��ֱ������Բ��λ�ù�ϵ��֪ʶ��������������ͷ���������������������ۺ���ǿ���ѶȽϴ�


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
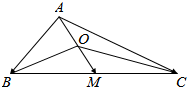 ��ͼ���ڡ�ABC�У�OΪ����AM�ϵĶ��㣮
��ͼ���ڡ�ABC�У�OΪ����AM�ϵĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | -$\frac{1}{2}$ | C�� | -$\frac{{\sqrt{3}}}{2}$ | D�� | -$\frac{{\sqrt{3}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f ��-n����f ��n-1����f ��n+1�� | B�� | f ��n+1����f ��-n����f ��n-1�� | ||
| C�� | f ��n-1����f ��-n����f ��n+1�� | D�� | f ��n+1����f ��n-1����f ��-n�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com