
【题目】椭圆规是用来画椭圆的一种器械,它的构造如图所示,在一个十字形的金属板上有两条互相垂直的导槽,在直尺上有两个固定的滑块A,B,它们可分别在纵槽和横槽中滑动,在直尺上的点M处用套管装上铅笔,使直尺转动一周,则点M的轨迹C是一个椭圆,其中|MA|=2,|MB|=1,如图,以两条导槽的交点为原点O,横槽所在直线为x轴,建立直角坐标系.
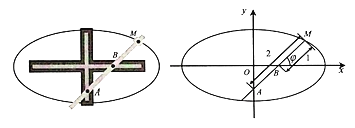
(1)将以射线Bx为始边,射线BM为终边的角xBM记为φ(0≤φ<2π),用![]() 表示点M的坐标,并求出C的普通方程;
表示点M的坐标,并求出C的普通方程;
(2)已知过C的左焦点F,且倾斜角为α(0≤α![]() )的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当
)的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当![]() ,|GH|,
,|GH|,![]() 依次成等差数列时,求直线l2的普通方程.
依次成等差数列时,求直线l2的普通方程.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)用三角函数表示出点M的坐标,直接利用转换关系把极坐标方程转换为直角坐标方程;(2)设出直线l1的参数方程,与椭圆方程联立利用直线参数的几何意义求出![]() 、
、![]() ,根据题意有
,根据题意有![]() ,列出方程求出直线l1的斜率即可求得直线l2的方程.
,列出方程求出直线l1的斜率即可求得直线l2的方程.
(1)设M(x,y)依题意得:x=2cosφ,y=sinφ,
所以M(2cosφ,sinφ),
由于cos2φ+sin2φ=1,整理得![]() .
.
(2)由于直线l1的倾斜角为α(![]() ),且l1⊥l2,
),且l1⊥l2,
所以直线l2的倾斜角为![]() ,依题意易知:F(
,依题意易知:F(![]() ),
),
可设直线l1的方程为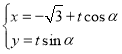 (t为参数),
(t为参数),
代入![]() 得到:
得到:![]() ,
,
易知![]() ,
,
设点D和点E对应的参数为t1和t2,
所以![]() ,
,![]() .
.
则![]() ,
,
由参数的几何意义: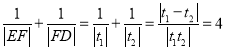 ,
,
设G、H对应的参数为t3和t4,同理对于直线l2,将α换为![]() ,
,
所以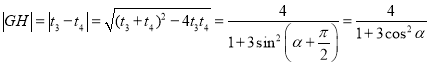 ,
,
由于![]() ,|GH|,
,|GH|,![]() 依次成等差数列,
依次成等差数列,
所以![]() ,则
,则![]() ,解得
,解得![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以直线l2的斜率为![]() ,直线l2的直角坐标方程为x
,直线l2的直角坐标方程为x![]() .
.


科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色其面积称为朱实,黄实,利朱用2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2,设勾股中勾股比为![]() ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
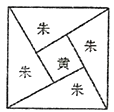
A.886B.500C.300D.134
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,侧面
中,侧面![]()
![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在求出
,若存在求出![]() 的长,若不存在说明理由.
的长,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() 1(a>0,b>0)的焦点分别为F1(﹣5,0),F2(5,0),P为C上一点,PF1⊥PF2,tan∠PF1F2
1(a>0,b>0)的焦点分别为F1(﹣5,0),F2(5,0),P为C上一点,PF1⊥PF2,tan∠PF1F2![]() ,则C的方程为( )
,则C的方程为( )
A.x2![]() 1B.
1B.![]() y2=1
y2=1
C.![]() 1D.
1D.![]() 1
1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级有男生![]() 人,学号为
人,学号为![]() ,
,![]() ,
,![]() ,
,![]() ;女生
;女生![]() 人,学号为
人,学号为![]() ,
,![]() ,
,![]() ,
,![]() .对高三学生进行问卷调查,按学号采用系统抽样的方法,从这
.对高三学生进行问卷调查,按学号采用系统抽样的方法,从这![]() 名学生中抽取
名学生中抽取![]() 人进行问卷调查(第一组采用简单随机抽样,抽到的号码为
人进行问卷调查(第一组采用简单随机抽样,抽到的号码为![]() );再从这
);再从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人进行数据分析,则这
人进行数据分析,则这![]() 人中既有男生又有女生的概率是( )
人中既有男生又有女生的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞的轻轨给市民出行带来了很大的方便,越来越多的市民选择乘坐轻轨出行,很多市民都会开汽车到离家最近的轻轨站,将车停放在轻轨站停车场,然后进站乘轻轨出行,这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题,决定对机动车停车施行收费制度,收费标准如下:4小时内(含4小时)每辆每次收费5元;超过4小时不超过6小时,每增加一小时收费增加3元;超过6小时不超过8小时,每增加一小时收费增加4元,超过8小时至24小时内(含24小时)收费30元;超过24小时,按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间(假设每辆车一天内在该停车场仅停车一次),得到下面的频数分布表:

以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.
(1)现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研,记录并统计了停车时长与司机性别的![]() 列联表:
列联表:

完成上述列联表,并判断能否有![]() 的把握认为“停车是否超过6小时”与性别有关?
的把握认为“停车是否超过6小时”与性别有关?
(2)(i)X表示某辆车一天之内(含一天)在该停车场停车一次所交费用,求X的概率分布列及期望![]() :
:
(ii)现随机抽取该停车场内停放的3辆车,![]() 表示3辆车中停车费用大于
表示3辆车中停车费用大于![]() 的车辆数,求P(
的车辆数,求P(![]() )的概率.
)的概率.
参考公式: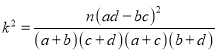 ,其中
,其中![]()
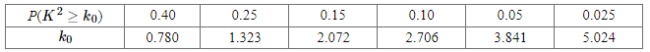
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高,2019年全年总收入与2018年全年总收入相比增长了一倍,同时该企业的各项运营成本也随着收入的变化发生相应变化,下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法错误的是( )
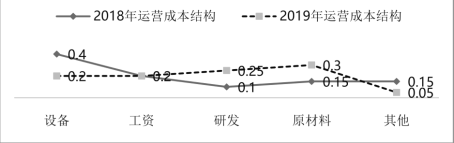
A.该企业2019年研发的费用与原材料的费用超过当年总收入的50%
B.该企业2019年设备支出金额及原材料的费用均与2018相当
C.该企业2019年工资支出总额比2018年多一倍
D.该企业2018年与2019研发的总费用占这两年总收入的20%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高二年级组织外出参加学业水平考试,出行方式为:乘坐学校定制公交或自行打车前往,大数据分析显示,当![]() 的学生选择自行打车,自行打车的平均时间为
的学生选择自行打车,自行打车的平均时间为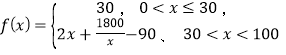 (单位:分钟) ,而乘坐定制公交的平均时间不受
(单位:分钟) ,而乘坐定制公交的平均时间不受![]() 影响,恒为40分钟,试根据上述分析结果回答下列问题:
影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
(2)求该校学生参加考试平均时间![]() 的表达式:讨论
的表达式:讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com