
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:平面![]() 面
面![]() ;
;
(Ⅱ)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
【答案】(I)详见解析;(II)![]() .
.
【解析】
(Ⅰ)由题意得到![]() 面
面![]() ,从而
,从而![]() .又由题意证得四边形
.又由题意证得四边形![]() 为菱形,故得
为菱形,故得![]() ,于是
,于是![]() 平面
平面![]() .根据面面垂直的判定定理可得结论成立.(Ⅱ)由题意得
.根据面面垂直的判定定理可得结论成立.(Ⅱ)由题意得![]() 为
为![]() 中点,建立空间直角坐标系,求出平面
中点,建立空间直角坐标系,求出平面![]() 和平面
和平面![]() 的法向量,根据两向量夹角的余弦值可得二面角的余弦值.
的法向量,根据两向量夹角的余弦值可得二面角的余弦值.
(Ⅰ)证明:因为![]() ,则
,则![]() ,
,
又侧面![]() 底面
底面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 面
面![]() .
.
因为![]() 平面
平面![]() ,则
,则![]() .
.
又因为![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,
则![]() ,又
,又![]()
则![]() 为等边三角形,则四边形
为等边三角形,则四边形![]() 为菱形,
为菱形,
所以![]() .
.
又![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 面
面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅱ)由平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,则
分成体积相等的两部分,则![]() 为
为![]() 中点.
中点.
由(Ⅰ)知![]() 面
面![]() ,且四边形
,且四边形![]() 为菱形、
为菱形、![]() .以A为原点建立如图所示的空间直角坐标系
.以A为原点建立如图所示的空间直角坐标系![]() ,
,
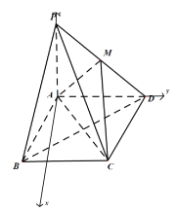
则![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,得
,得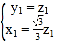 ,
,
令![]() ,可得
,可得![]() .
.
同理,平面![]() 的法向量
的法向量![]() .
.
所以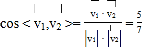 .
.
由图形得二面角![]() 为钝角,
为钝角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线y=ax+1和抛物线y2=4x相交于不同的A,B两点.
(Ⅰ)若a=-2,求弦长|AB|;
(Ⅱ)若以AB为直径的圆经过原点O,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() ,
,![]() ,…,
,…,![]() 是一个数列,对每个
是一个数列,对每个![]() ,
,![]() ,
,![]() .如果
.如果![]() ,
,![]() 两数不同,写
两数不同,写![]() ;如果
;如果![]() ,
,![]() 两数相同,写
两数相同,写![]() .于是得到一个新数列
.于是得到一个新数列![]() ,
,![]() ,…,
,…,![]() ,其中
,其中![]() .重复上述方法,得到一个由0及1两个数字组成的三角形数表,最后一行仅一个数字,求这张数字表中1的和的最大值.
.重复上述方法,得到一个由0及1两个数字组成的三角形数表,最后一行仅一个数字,求这张数字表中1的和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某校九年级400名学生的体质情况,随机抽查了20名学生,测试1 min仰卧起坐的成绩(次数),测试成绩如下:
30 35 32 33 28 36 34 28 25 40
28 32 30 42 37 36 33 31 26 24
(1)20名学生的平均成绩![]() 是多少?标准差
是多少?标准差![]() 是多少?
是多少?
(2)次数位于![]() 与
与![]() 之间有多位同学?所占的百分比是多少?
之间有多位同学?所占的百分比是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类似于平面直角坐标系,定义平面斜坐标系:设数轴![]() 、
、![]() 的交点为
的交点为![]() ,与
,与![]() 、
、![]() 轴正方向同向的单位向量分别是
轴正方向同向的单位向量分别是![]() 、
、![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ,其中
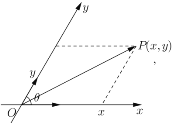
,其中![]() ,由平面向量基本定理:对于平面内的向量
,由平面向量基本定理:对于平面内的向量![]() ,存在唯一有序实数对
,存在唯一有序实数对![]() ,使得
,使得![]() ,把
,把![]() 叫做点
叫做点![]() 在斜坐标系
在斜坐标系![]() 中的坐标,也叫做向量
中的坐标,也叫做向量![]() 在斜坐标系
在斜坐标系![]() 中的坐标,记为
中的坐标,记为![]() ,在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如
,在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如![]() 时,方程
时,方程![]() 表示斜坐标系内一条过点
表示斜坐标系内一条过点![]() ,且方向向量为
,且方向向量为![]() 的直线.
的直线.
(1)若![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() ,已知点
,已知点![]() 和直线
和直线![]() ;
;
①求![]() 的一个法向量;
的一个法向量;
②求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题统计结果如图表所示.
人,回答问题统计结果如图表所示.
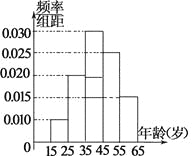
组号 | 分组 | 回答正确 | 回答正确的人数 |
第1组 |
| 5 | 0.5 |
第2组 |
|
| 0.9 |
第3组 |
| 27 |
|
第4组 |
|
| 0.36 |
第5组 |
| 3 |
|
(Ⅰ) 分别求出![]() 的值;
的值;
(Ⅱ) 从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(Ⅲ) 在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域存在实数
,若在定义域存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() (
(![]()
![]() ),试判断
),试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若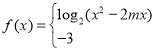
![]() 为其定义域上的“局部奇函数”,求实数
为其定义域上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com