
【题目】已知动点![]() 到两定点
到两定点![]() ,
,![]() 距离之和为4(
距离之和为4(![]() ),且动点
),且动点![]() 的轨迹曲线
的轨迹曲线![]() 过点
过点![]() .
.
(1)求![]() 的值;
的值;
(2)若直线![]() 与曲线
与曲线![]() 有不同的两个交点
有不同的两个交点![]() ,且
,且![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的值.
的值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】用“算筹”表示数是我国古代计数方法之一,计数形式有纵式和横式两种,如图1所示.金元时期的数学家李治在《测圆海镜》中记载:用“天元术”列方程,就是用算筹来表示方程中各项的系数.所谓“天元术”,即是一种用数学符号列方程的方法,“立天元一为某某”,意即“设![]() 为某某”.如图2所示的天元式表示方程
为某某”.如图2所示的天元式表示方程![]() ,其中
,其中![]() 表示方程各项的系数,均为筹算数码,在常数项旁边记一“太”字或在一次项旁边记一“元”字,“太”或“元”向上每层减少一次幂,向下每层增加一次幂.试根据上述数学史料,判断图3所示的天元式表示的方程是________________
表示方程各项的系数,均为筹算数码,在常数项旁边记一“太”字或在一次项旁边记一“元”字,“太”或“元”向上每层减少一次幂,向下每层增加一次幂.试根据上述数学史料,判断图3所示的天元式表示的方程是________________

查看答案和解析>>
科目:高中数学 来源: 题型:
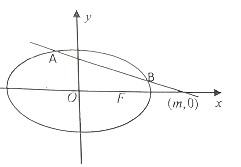
【题目】已知椭圆![]() 的右焦点F与抛物线
的右焦点F与抛物线![]() 焦点重合,且椭圆的离心率为
焦点重合,且椭圆的离心率为![]() ,过
,过![]() 轴正半轴一点
轴正半轴一点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的标准方程;
(2)是否存在实数![]() 使以线段
使以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在说明理由.
的值;若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 |
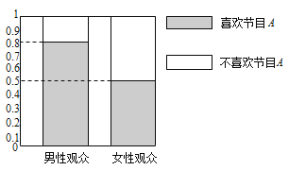
(1)根据该等高条形图,完成右上![]() 列联表,并用独立性检验的方法分析,则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?
(2)从男性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附: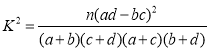
| 0.100 | 0.050 | 0.010 | 0.00 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动支付的普及,中国人的生活方式正悄然巨变,带智能手机,不带钱包出门还渐成为中国人的新习惯![]() 年我国移动支付增长迅猛,据统计,某支付平台2017年移动支付的笔数占总支付笔数的
年我国移动支付增长迅猛,据统计,某支付平台2017年移动支付的笔数占总支付笔数的![]() .
.
![]() Ⅰ
Ⅰ![]() 从该支付平台2017年的所有支付中任取10笔,求移动支付笔数的期望和方差;
从该支付平台2017年的所有支付中任取10笔,求移动支付笔数的期望和方差;
![]() Ⅱ
Ⅱ![]() 现有500名使用该支付平台的用户,其中300名是城市用户,200名是农村用户,调查他们2017年个人移动支付的比例是否达到了
现有500名使用该支付平台的用户,其中300名是城市用户,200名是农村用户,调查他们2017年个人移动支付的比例是否达到了![]() ,得到
,得到![]() 列联表如下:
列联表如下:
个人移动支付达到了 | 个人移动支付达到了 | 合计 | |
城市用户 | 270 | 30 | 300 |
农村用户 | 170 | 30 | 200 |
合计 | 440 | 60 | 500 |
根据上表数据,问是否有![]() 的把握认为2017年个人移动支付比例达到了
的把握认为2017年个人移动支付比例达到了![]() 与该用户是城市用户还是农村用户有关?
与该用户是城市用户还是农村用户有关?
附:![]()
|
|
|
k |
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com