考点:直线与平面所成的角,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离,空间角
分析:(1)由正方体的结构特征,结合已知中过BD1的平面分别交棱AA1和棱CC1于E、F两点,根据面面平行的性质定理,可得D1E∥BF,BE∥D1F,即四边形EBFD1为平行四边形,进而由HL可证得Rt△A1D1E≌Rt△CB,由全等三角形的性质可得A1E=CF,AE=CF,由此能证明截面BED1F把正方体分成体积相等的两部分.
(2)以DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出直线BD与平面BED1F所成角的正弦值.
解答:
(1)证明:由题知,平面EBFD
1与平面BCC
1B
1交于BF、与平面ADD
1A交于ED
1,
又平面BCC
1B
1∥平面ADD
1A
1∴D
1E∥BF,同理BE∥D
1F,

∴四边形EBFD
1为平行四边形
∴D
1E=BF,
∵A
1D
1=CB,D
1E=BF,
∠D
1A
1E=∠BCF=90°
∴Rt△A
1D
1E≌Rt△CBF
∴A
1E=CF,AE=CF,
∴截面BED
1F把正方体分成体积相等的两部分.
(2)解:以DA为x轴,DC为y轴,
DD
1为z轴,建立空间直角坐标系,
设AE=t,则CF=1-t(0≤t≤1),
B(1,1,0),D
1(0,0,1),E(1,0,t),
=(-1,-1,1),
=(0,-1,t),
设平面BED
1F的法向量
=(x,y,z),
则
,取y=1,得
=(
-1,1,
),
平面ABCD的法向量
=(0,0,1),
∵截面BED
1F与底面ABCD所成二面角的余弦值为
,
∴|cos<
,>|=|
|=
,
解得t=
,平面BED
1F的法向量
=(1,1,2),
=(-1,-1,0),
设直线BD与平面BED
1F所成角为θ,
sinθ=|cos<
,>|=|
|=
,
∴直线BD与平面BED
1F所成角的正弦值为
.
点评:本题考查截面BED1F把正方体分成体积相等的两部分的证明,考查直线BD与平面BED1F所成角的正弦值的求法,解题时要注意向量法的合理运用.

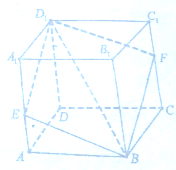 如图,在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的平面分别交AA1,CC1于点E,F.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的平面分别交AA1,CC1于点E,F.


 全优点练单元计划系列答案
全优点练单元计划系列答案 已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍,且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.
已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍,且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.