考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由四边形A1ABB1为菱形,得对角线AB1⊥A1B,由侧面A1ABB1⊥底面ABC,∠ABC=90°,得CB⊥侧面A1ABB1,从而CB⊥AB1,由此能证明AB1⊥平面A1BC.
(Ⅱ)由勾股定理得AB=4,由菱形A1ABB1中∠A1AB=60°,得△A1AB为正三角形,以菱形A1ABB1的对角线交点O为坐标原点OA1方向为x轴,OA方向为y轴,过O且与BC平行的方向为z 轴建立如图空间直角坐标系,分别求出平面A1CC1的法向量和平面A1BC的法向量,由此能求出二面角B-A1C-C1的余弦值.
解答:
(Ⅰ)证明:在侧面A
1ABB
1中,因为A
1A=AB,

所以四边形A
1ABB
1为菱形,
所以对角线AB
1⊥A
1B,…(2分)
因为侧面A
1ABB
1⊥底面ABC,∠ABC=90°,
所以CB⊥侧面A
1ABB
1,
因为AB
1?平面A
1ABB
1内,所以CB⊥AB
1,…(4分)
又因为A
1B∩BC=B,
所以AB
1⊥平面A
1BC. …(6分)
(Ⅱ)解:在Rt△ABC中,AC=5,BC=3,
所以AB=
=4,
又菱形A
1ABB
1中,因为∠A
1AB=60°,所以△A
1AB为正三角形,
如图,以菱形A
1ABB
1的对角线交点O为坐标原点OA
1方向为x轴,OA方向为y轴,
过O且与BC平行的方向为z 轴建立如图空间直角坐标系,
则A
1(2,0,0),B(-2,0,0),C(-2,0,3),
B
1(0,-2
,0),C
1(0,-2
,3),
∴
=(-2,2
,0),
=(2,2
,-3),
设
=(x,y,z)为平面A
1CC
1的法向量,
则
,取x=3,得
=(3,
,4),
又
=(0,-2
,0)是平面A
1BC的一个法向量,
∴cos<
,>=
=
=-
,
∴二面角B-A
1C-C
1的余弦值为-
.…(12分)
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,涉及到线线、线面、面面平行与垂直的性质、勾股定理、向量法等知识点的合理运用,是中档题.

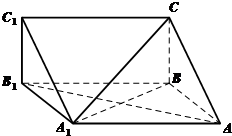 如图,在三棱柱ABC-A1B1C1中,AA1=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.
如图,在三棱柱ABC-A1B1C1中,AA1=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC.


 已知抛物线C的顶点在原点,焦点在y轴上,抛物线上点M(x,4)(x>0)到准线的距离是5.
已知抛物线C的顶点在原点,焦点在y轴上,抛物线上点M(x,4)(x>0)到准线的距离是5.