
【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ2(cos2θ+3sin2θ)=12,直线l的参数方程为![]() (t为参数),直线l与曲线C交于M,N两点.
(t为参数),直线l与曲线C交于M,N两点.
(1)若点P的极坐标为(2,π),求|PM||PN|的值;
(2)求曲线C的内接矩形周长的最大值.
【答案】(1)![]() (2)16
(2)16
【解析】
(1)利用极坐标转化为直角坐标的公式,求得曲线![]() 的直角坐标方程.求得
的直角坐标方程.求得![]() 的直角坐标,由此判断
的直角坐标,由此判断![]() 在直线
在直线![]() 上,求得直线
上,求得直线![]() 的标准参数方程,代入曲线
的标准参数方程,代入曲线![]() 的直角坐标方程,化简后写出韦达定理,结合直线参数的几何意义,求得
的直角坐标方程,化简后写出韦达定理,结合直线参数的几何意义,求得![]() 的值.
的值.
(2)求得椭圆![]() 内接矩形周长的表达式,结合三角函数最值的求法,求得周长的最大值.
内接矩形周长的表达式,结合三角函数最值的求法,求得周长的最大值.
(1)曲线C的极坐标方程为ρ2(cos2θ+3sin2θ)=12,转换为直角坐标方程为![]() .
.
点P的极坐标为(2,π),转换为直角坐标为(﹣2,0)由于点P(﹣2,0)在直线l上,
所以直线l的参数方程为![]() (t为参数),转化为
(t为参数),转化为 (t为参数),
(t为参数),
所以代入曲线的方程为![]() ,
,
整理得![]() ,
,
所以|PM||PN|=|t1t2|=4.
(2)不妨设Q(![]() ),(
),(![]() ),
),
所以该矩形的周长为4(![]() )=16sin(
)=16sin(![]() ).
).
当![]() 时,矩形的周长的最大值为16.
时,矩形的周长的最大值为16.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】某调查机构为了了解某产品年产量x(吨)对价格y(千克/吨)和利润z的影响,对近五年该产品的年产量和价格统计如下表:
x | 1 | 2 | 3 | 4 | 5 |
y | 17.0 | 16.5 | 15.5 | 13.8 | 12.2 |
(1)求y关于x的线性回归方程![]() ;
;
(2)若每吨该产品的成本为12千元,假设该产品可全部卖出,预测当年产量为多少时,年利润w取到最大值?
参考公式: 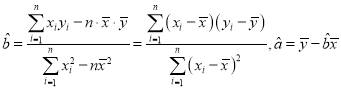
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取了100名高中生,根据问卷调查,得到以下数据:
作文成绩优秀 | 作文成绩一般 | 总计 | |
课外阅读量较大 | 35 | 20 | 55 |
课外阅读量一般 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
(1)根据列联表,能否有99.5%的把握认为课外阅读量的大小与作文成绩优秀有关;
(2)若用分层抽样的方式从课外阅读量一般的高中生中选取了6名高中生,再从这6名高中生中随机选取2名进行面谈,求面谈的高中生中至少有1名作文成绩优秀的概率.
附: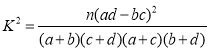 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》有着丰富多彩的内容,是了解我国古代数学的重要文献.这5部专著中有3部产生于汉、魏、晋、南北朝时期.现拟从这5部专著中选择2部作为学生课外兴趣拓展参考书目,则所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜批发商经销某种新鲜蔬菜(以下简称![]() 蔬菜),购入价为200元/袋,并以300元/袋的价格售出,若前8小时内所购进的
蔬菜),购入价为200元/袋,并以300元/袋的价格售出,若前8小时内所购进的![]() 蔬菜没有售完,则批发商将没售完的
蔬菜没有售完,则批发商将没售完的![]() 蔬菜以150元/袋的价格低价处理完毕(根据经验,2小时内完全能够把
蔬菜以150元/袋的价格低价处理完毕(根据经验,2小时内完全能够把![]() 蔬菜低价处理完,且当天不再购进).该蔬菜批发商根据往年的销量,统计了100天
蔬菜低价处理完,且当天不再购进).该蔬菜批发商根据往年的销量,统计了100天![]() 蔬菜在每天的前8小时内的销售量,制成如下频数分布条形图.
蔬菜在每天的前8小时内的销售量,制成如下频数分布条形图.

(1)若某天该蔬菜批发商共购入6袋![]() 蔬菜,有4袋
蔬菜,有4袋![]() 蔬菜在前8小时内分别被4名顾客购买,剩下2袋在8小时后被另2名顾客购买.现从这6名顾客中随机选2人进行服务回访,则至少选中1人是以150元/袋的价格购买的概率是多少?
蔬菜在前8小时内分别被4名顾客购买,剩下2袋在8小时后被另2名顾客购买.现从这6名顾客中随机选2人进行服务回访,则至少选中1人是以150元/袋的价格购买的概率是多少?
(2)以上述样本数据作为决策的依据.
(i)若今年![]() 蔬菜上市的100天内,该蔬菜批发商坚持每天购进6袋
蔬菜上市的100天内,该蔬菜批发商坚持每天购进6袋![]() 蔬菜,试估计该蔬菜批发商经销
蔬菜,试估计该蔬菜批发商经销![]() 蔬菜的总盈利值;
蔬菜的总盈利值;
(ii)若明年该蔬菜批发商每天购进![]() 蔬菜的袋数相同,试帮其设计明年的
蔬菜的袋数相同,试帮其设计明年的![]() 蔬菜的进货方案,使其所获取的平均利润最大.
蔬菜的进货方案,使其所获取的平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请全校
的值:先请全校![]() 名同学每人随机写下一个都小于
名同学每人随机写下一个都小于![]() 的正实数对
的正实数对![]() ;再统计两数能与
;再统计两数能与![]() 构成钝角三角形三边的数对
构成钝角三角形三边的数对![]() 的个数
的个数![]() ;最后再根据统计数
;最后再根据统计数![]() 估计
估计![]() 的值,那么可以估计
的值,那么可以估计![]() 的值约为( )
的值约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
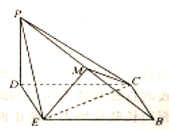
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光伏发电是将光能直接转变为电能的一种技术,具有资源的充足性及潜在的经济性等优点,在长期的能源战略中具有重要地位,2015年起,国家能源局、国务院扶贫办联合在6省的30个县开展光伏扶贫试点,在某县居民中随机抽取50户,统计其年用量得到以下统计表.以样本的频率作为概率.
用电量(单位:度) |
|
|
|
|
|
户数 | 7 | 8 | 15 | 13 | 7 |
(Ⅰ)在该县居民中随机抽取10户,记其中年用电量不超过600度的户数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(Ⅱ)在总结试点经验的基础上,将村级光伏电站稳定为光伏扶贫的主推方式.已知该县某自然村有居民300户.若计划在该村安装总装机容量为300千瓦的光伏发电机组,该机组所发电量除保证该村正常用电外,剩余电量国家电网以0.8元/度的价格进行收购.经测算每千瓦装机容量的发电机组年平均发电1000度,试估计该机组每年所发电量除保证正常用电外还能为该村创造直接受益多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com