
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
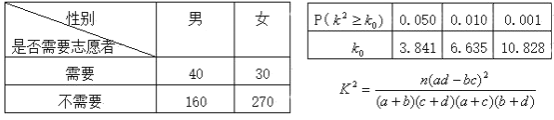
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
科目:高中数学 来源: 题型:
【题目】南康某服装厂拟在![]() 年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)
年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元满足
万元满足![]() .已知
.已知![]() 年生产该产品的固定投入为
年生产该产品的固定投入为![]() 万元,每生产
万元,每生产![]() 万件该产品需要再投入
万件该产品需要再投入![]() 万元.厂家将每件产品的销售价格定为每件产品年平均成本的
万元.厂家将每件产品的销售价格定为每件产品年平均成本的![]() 倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将![]() 年该产品的利润
年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该服装厂![]() 年的促销费用投入多少万元时,利润最大?
年的促销费用投入多少万元时,利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,点
,点![]() 是动点,且直线
是动点,且直线![]() 和直线
和直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 与(1)中轨迹相切于点
与(1)中轨迹相切于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,判断以
,判断以![]() 为直径的圆是否过
为直径的圆是否过![]() 轴上一定点?
轴上一定点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的公差d>0,则下列四个命题:
的公差d>0,则下列四个命题:
①数列![]() 是递增数列; ②数列
是递增数列; ②数列![]() 是递增数列;
是递增数列;
③数列![]() 是递增数列; ④数列
是递增数列; ④数列![]() 是递增数列.
是递增数列.
其中正确命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a、b、c分别是角A、B、C的对边,S是该三角形的面积,且![]()
(1)求角A的大小;
(2)若角A为锐角, ![]() ,求边BC上的中线AD的长.
,求边BC上的中线AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,△ABC是等边三角形,AB⊥AD,CB⊥CD,点P是AC的中点,记△BPD、△ABD的面积分别为
中,△ABC是等边三角形,AB⊥AD,CB⊥CD,点P是AC的中点,记△BPD、△ABD的面积分别为![]() ,
,![]() ,二面角A-BD-C的大小为
,二面角A-BD-C的大小为![]() ,
,
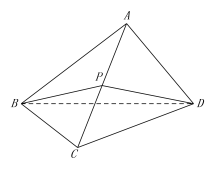
证明:(Ⅰ)平面ACD![]() 平面BDP;
平面BDP;
(Ⅱ)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三全体![]() 名学生中随机抽取了
名学生中随机抽取了![]() 名学生的体检表,并得到如图所示的频率分布直方图.
名学生的体检表,并得到如图所示的频率分布直方图.
(Ⅰ)若直方图中后四组的频数成等差数列,计算高三全体学生视力在![]() 以下的人数,并估计这
以下的人数,并估计这![]() 名学生视力的中位数(精确到
名学生视力的中位数(精确到![]() );
);
(Ⅱ)学习小组发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对高三全体成绩名次在前![]() 名和后
名和后![]() 名的学生进行了调查,部分数据如表1,根据表1及临界表2中的数据,能否在犯错误的概率不超过
名的学生进行了调查,部分数据如表1,根据表1及临界表2中的数据,能否在犯错误的概率不超过![]() 的前提下认为视力与学习成绩有关系?
的前提下认为视力与学习成绩有关系?

年段名次 是否近视 | 前 | 后 |
近 视 |
| |
|
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
(参考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年元旦期间,某运动服装专卖店举办了一次有奖促销活动,消费每超过400元均可参加1次抽奖活动,抽奖方案有两种,顾客只能选择其中的一种.
方案一:顾客转动十二等分且质地均匀的圆形转盘(如图),转盘停止转动时指针指向哪个扇形区域,则顾客可直接获得该区域对应面额(单位:元)的现金优惠,且允许顾客转动3次.
方案二:顾客转动十二等分且质地均匀的圆形转盘(如图〕,转盘停止转动时指针若指向阴影部分,则未中奖,若指向白色区域,则顾客可直接获得40元现金,且允许顾客转动3次.

(1)若两位顾客均获得1次抽奖机会,且都选择抽奖方案一,试求这两位顾客均获得180元现金优惠的概率;
(2)若某顾客恰好获得1次抽奖机会.
①试分别计算他选择两种抽奖方案最终获得现金奖励的数学期望;
②从概率的角度比较①中该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com