已知圆x2+y2-6mx-2(m-1)y+10m2-2m-24=0,直线l1:x-3y-3=0
(1)求证:不论m取何值,圆心必在直线l1上;
(2)与l1平行的直线中,哪些与圆相交、相切、相离.
解:(1)圆x
2+y
2-6mx-2(m-1)y+10m
2-2m-24=0,
配方得(x-3m)
2+[y-(m-1)]
2=25,…(2分)
∴圆心为(3m,m-1),半径为 5.…(3分)
∵3m-3(m-1)-3=0,∴不论m取何值,圆心必在直线l
1:x-3y-3=0上.…(5分)
(2)设与直线l
1平行的直线l
2:x-3y+b=0(b≠-3),…(6分)
则圆心到直线l
2的距离为
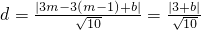
.…(8分)
∴当d<r,即

,

且b≠-3时,直线与圆相交;
当d=r,即

,

或
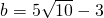
时,直线与圆相切;
当d>r,即
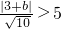
,
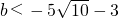
或
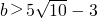
时,直线与圆相离.…(14分)
分析:(1)把圆的方程化为标准方程求出圆心和半径,经检验,圆心必在直线l
1:x-3y-3=0上.
(2)设出与直线l
1平行的直线l
2的方程,求出圆心到直线l
2的距离,当d<r时,直线和圆相交,当d=r,直线和圆相切,
当d>r,直线与圆相离.
点评:本题主要考查圆的标准方程的特征,直线和圆的位置关系的判断方法,属于中档题.

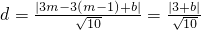 .…(8分)
.…(8分) ,
, 且b≠-3时,直线与圆相交;
且b≠-3时,直线与圆相交; ,
, 或
或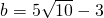 时,直线与圆相切;
时,直线与圆相切;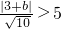 ,
,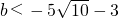 或
或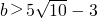 时,直线与圆相离.…(14分)
时,直线与圆相离.…(14分)

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案