
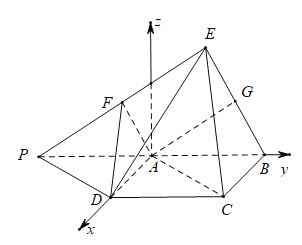
【题目】在如图所示的六面体中,四边形![]() 是边长为
是边长为![]() 的正方形,四边形
的正方形,四边形![]() 是梯形,
是梯形,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
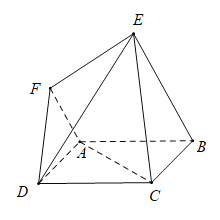
(1)在图中作出平面 ![]() 与平面
与平面![]() 的交线,并写出作图步骤,但不要求证明;
的交线,并写出作图步骤,但不要求证明;
(2)求证:![]() 平面
平面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 所成角的余弦值
所成角的余弦值
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)延长![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,根据公理
,根据公理![]() 和公理
和公理![]() 可知,
可知,![]() 即是所求.
即是所求.
(2)通过证明四边形![]() 是平行四边形,证得
是平行四边形,证得![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(3)利用勾股定理计算出![]() ,建立空间直角坐标系,通过平面
,建立空间直角坐标系,通过平面![]() 和平面
和平面![]() 的法向量,计算出二面角的余弦值.
的法向量,计算出二面角的余弦值.
(1)延长![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,则直线
,则直线 ![]() 就是平面
就是平面![]() 与平面
与平面![]() 的交线.
的交线.
(2)因为![]() ,
,![]() ,所以
,所以![]() 是
是![]() 的中位线,故
的中位线,故![]() ,
,
因为![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
因为![]() 面
面![]() ,
,![]() 面
面![]() ,
,
所以![]() 平面
平面![]() .
.
(3)在平面![]() 内,过点
内,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,又
,又![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,![]() ,
,![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
所以![]() 为直角三角形,
为直角三角形,
且![]() ,
,![]() ,
,![]() .
.
在平面![]() 内,过点
内,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,
,
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 面
面![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 的方向为
的方向为![]() 轴正方向,
轴正方向,![]() 的方向为
的方向为![]() 轴正方向,建立如图所示的空间直角坐标系
轴正方向,建立如图所示的空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,设
,设![]() 是平面
是平面![]() 的法向量,
的法向量,
则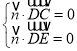 ,即
,即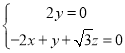 ,所以可取
,所以可取![]() .
.
因为![]() 是平面
是平面![]() 的法向量,
的法向量,
所以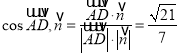 ,
,
所以平面![]() 与平面
与平面![]() 所成角的余弦值
所成角的余弦值![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() .
.
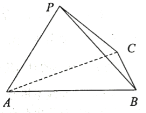
(1)若![]() ,求证:平面
,求证:平面![]() 平面PBC;
平面PBC;
(2)若PA与平面ABC所成的角为![]() ,求二面角C-PB-A的余弦值.
,求二面角C-PB-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩是中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有1300多年的历史,制作工艺十分复杂,而且优质品检验异常严格,检验方案是:先从烧制的这批唐三彩中任取 3件作检验,这3件唐三彩中优质品的件数记为![]() .如果
.如果![]() ,再从这批唐三彩中任取3件作检验,若都为优质品,则这批唐三彩通过检验;如果
,再从这批唐三彩中任取3件作检验,若都为优质品,则这批唐三彩通过检验;如果![]() ,再从这批唐三彩中任取1件作检验,若为优质品,则这批唐三彩通过检验;其他情况下,这批唐三彩都不能通过检验.假设这批唐三彩的优质品概率为
,再从这批唐三彩中任取1件作检验,若为优质品,则这批唐三彩通过检验;其他情况下,这批唐三彩都不能通过检验.假设这批唐三彩的优质品概率为![]() ,即取出的每件唐三彩是优质品的概率都为
,即取出的每件唐三彩是优质品的概率都为![]() ,且各件唐三彩是否为优质品相互独立.
,且各件唐三彩是否为优质品相互独立.
(1)求这批唐三彩通过优质品检验的概率;
(2)已知每件唐三彩的检验费用为100元,且抽取的每件唐三彩都需要检验,对这批唐三彩作质量检验所需的总费用记为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的渐近线方程为y=±
(a>0,b>0)的渐近线方程为y=±![]() x,右顶点为(1,0).
x,右顶点为(1,0).
(1)求双曲线C的方程;
(2)已知直线y=x+m与双曲线C交于不同的两点A,B,且线段AB的中点为![]() ,当x0≠0时,求
,当x0≠0时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能.近几年在国内出台的光伏发电补贴政策的引导下,某地光伏发电装机量急剧上涨,如下表:

某位同学分别用两种模型:①![]() ②
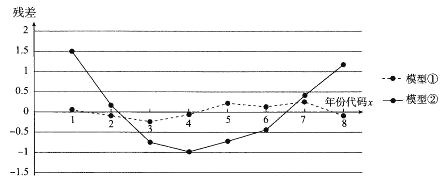
②![]() 进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于
进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于![]() ):
):
经过计算得![]() ,
,![]() .
.
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由.
(2)根据(1)的判断结果及表中数据建立y关于x的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
附:归直线的斜率和截距的最小二乘估计公式分别为: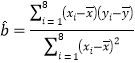 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是古代中国劳动人民发明的一种中国传统智力玩具,它由五块等腰直角三角形,一块正方形和一块平行四边形共七块板组成.清陆以湉《冷庐杂识》卷一中写道:近又有七巧图,其式五,其数七,其变化之式多至千余.体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自阴影部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() :
:![]() ,过抛物线焦点
,过抛物线焦点![]() 且与
且与![]() 轴垂直的直线与抛物线相交于
轴垂直的直线与抛物线相交于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 过焦点
过焦点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 、
、![]() ,切线
,切线![]() 与
与![]() 相交于点
相交于点![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]()
![]() 分别是椭圆的左右焦点,点
分别是椭圆的左右焦点,点![]() 是椭圆上任意一点,且
是椭圆上任意一点,且![]() .
.
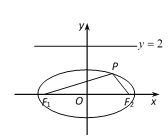
(Ⅰ)求椭圆的标准方程;
(Ⅱ)在直线![]() 上是否存在点Q,使以
上是否存在点Q,使以![]() 为直径的圆经过坐标原点O,若存在,求出线段
为直径的圆经过坐标原点O,若存在,求出线段![]() 的长的最小值,若不存在,请说明理由.
的长的最小值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com