




 种选法;第二步,乙则只需从甲选后剩下的7道题中任选6道,共有
种选法;第二步,乙则只需从甲选后剩下的7道题中任选6道,共有 种选法;
种选法; 种不同选法;
种不同选法; 种选法,第二步,乙只能选剩下的6道题,有一种选法;
种选法,第二步,乙只能选剩下的6道题,有一种选法; 种不同选法;
种不同选法; 个
个

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:浙江省富阳市新登中学2012届高三上学期期中考试数学理科试题 题型:022
2011年浙江省新课程自选模块考试试卷中共有18道试题,要求考生从中选取6道题进行解答,其中考生甲第1,2,9,15,16,17,18题一定不选,考生乙第3,9,15,16,17,18题一定不选,且考生甲与乙选取的6道题没有一题是相同的,则满足条件的选法种数共有________.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
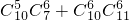
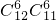
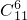
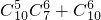
查看答案和解析>>
科目:高中数学 来源:浙江省学军中学2010届高三上学期第四次月考(理) 题型:填空题
2009年浙江省新课程自选模块考试试卷中共有18道试题,要求考生从中选取6道题 进行解答,其中考生甲第1,2,9,15,16,17,18题一定不选,考生乙第3,9,15,16,17,18题一定不选,且考生甲与乙选取的6道题没有一题是相同的,则满足条件的选法种数共有 . (用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com