练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．在△ABC中，若sin（A-B）=1+2cos（B+C）sin（A+C），则△ABC的形状一定是（　　）
    A．等边三角形B．不含60°的等腰三角形
    C．钝角三角形D．直角三角形

    分析 利用三角形内角和定理、诱导公式、和差公式即可得出．

    解答 解：∵sin（A-B）=1+2cos（B+C）sin（A+C），
    ∴sinAcosB-cosAsinB=1-2cosAsinB，
    ∴sinAcosB+cosAsinB=1，
    ∴sin（A+B）=1，
    ∴sinC=1．
    ∵C∈（0，π），
    ∴$C=\frac{π}{2}$．
    ∴△ABC的形状一定是直角三角形．
    故选：D．

    点评 本题考查了三角形内角和定理、诱导公式、和差公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    15．已知α∈（$\frac{π}{2}$，π），sinα=$\frac{3}{5}$，则tan（α+$\frac{3π}{4}$）=-7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．把正整数按“S”型排成了如图所示的三角形数表，第n行有n个数，对于第n行按从左往右的顺序依次标记第1列，第2列，…，第m列，（比如三角形数表中12在第5行第4列，18在第6行第3列），则三角形数表中2015在（　　）
    A．第63行第2列B．第62行第12列C．第64行第30列D．第64行第60列

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下列4个命题，其中正确的命题序号为（　　）
    ①|x+$\frac{1}{x}$|的最小值是2  ②$\frac{{x}^{2}+2}{\sqrt{{x}^{2}+1}}$的最小值是2  ③log2x+logx2的最小值是2   ④3x+3-x的最小值是2．
    A．①②③B．①②④C．②③④D．①③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．把正整数按一定的规律排成了如图所示的三角形数，设aij（i，j∈N+）是位于这个三角形数中从上往下数第i行，从左往右数第j列的数，如a32=5，若aij=2015，则i+j=（　　）
    A．111B．110C．108D．105

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．执行如图所示的程序框图，则输出S的结果是（　　）
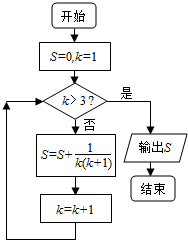
    A．$\frac{2}{3}$B．$\frac{3}{4}$C．$\frac{4}{5}$D．$\frac{5}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设函数f（x）=lg（1-2x）的定义域为集合M，g（x）=$\sqrt{4-{2}^{x}}$的定义域为集合N，记P=（∁RM）∩N．
    （1）求P；
    （2）求函数h（x）=log2x2+1（x∈P）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知tanα=2，tanβ=$\frac{1}{3}$，π＜α＜$\frac{3π}{2}$，0＜β＜π，则α-β的值为$\frac{5π}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．在△ABC中，角A，B，C所对的边分别为a，b，c，且（b-$\sqrt{2}c$）cosA+acosB=0．
    （1）求角A，
    （2）若a=$\sqrt{10}$，cosB=$\frac{2\sqrt{5}}{5}$，D为AC的中点，求BD的长度．

    查看答案和解析>>

    同步练习册答案