
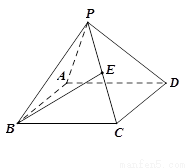
.如图所示,正四棱锥![]() P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为
P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为![]() .
.
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值;
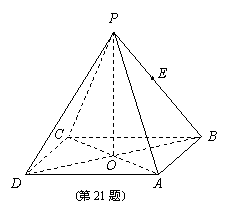 (3)问在棱AD上是否存在一点F,使EF⊥侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.
(3)问在棱AD上是否存在一点F,使EF⊥侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.
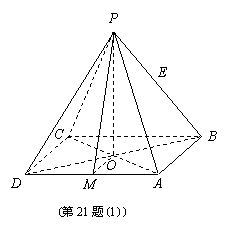 解:(1)取AD中点M,连接MO,PM,
解:(1)取AD中点M,连接MO,PM,
依条件可知AD⊥MO,AD⊥PO,
则∠PMO为所求二面角P-AD-O的平面角.
∵ PO⊥面ABCD,
∴∠PAO为侧棱PA与底面ABCD所成的角.
∴tan∠PAO=![]() .
.
设AB=a,AO=![]() a,
a,![]()
 ∴ PO=AO·tan∠POA=
∴ PO=AO·tan∠POA=![]() a,
a,
tan∠PMO=![]() =
=![]() .
.
∴∠PMO=60°.
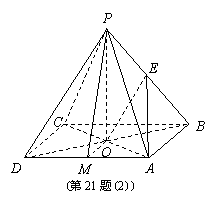
(2)连接AE,OE, ∵OE∥PD,
∴∠OEA为异面直线PD与AE所成的角.
∵AO⊥BD,AO⊥PO,∴AO⊥平面PBD.又OE![]() 平面PBD,∴AO⊥OE.
平面PBD,∴AO⊥OE.
∵OE=![]() PD=
PD=![]()
![]() =
=![]() a,
a,
∴tan∠AEO=![]() =
=![]() .
.
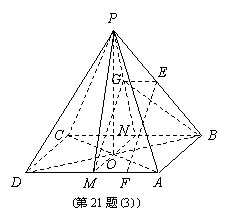
(3)延长MO交BC于N,取PN中点G,连BG,EG,MG.
∵BC⊥MN,BC⊥PN,∴BC⊥平面PMN.
∴平面PMN⊥平面PBC.
又PM=PN,∠PMN=60°,∴△PMN为正三角形.∴MG⊥PN.又平面PMN ∩平面PBC=PN,∴MG⊥平面PBC.
取AM中点F,∵EG∥MF,∴MF=![]() MA=EG,∴EF∥MG.
MA=EG,∴EF∥MG.
∴EF⊥平面PBC.点F为AD的四等分点.


科目:高中数学 来源: 题型:
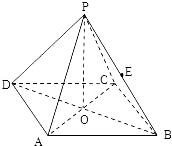 如图所示,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成的角的正切值为
如图所示,正四棱锥P-ABCD中,侧棱PA与底面ABCD所成的角的正切值为
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•南京二模)一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点p为顶点,加工成一个如图所示的正四棱锥形容器.当x=6cm时,该容器的容积为
(2012•南京二模)一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点p为顶点,加工成一个如图所示的正四棱锥形容器.当x=6cm时,该容器的容积为查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,正四棱锥P—ABCD的各棱长均为13,M,N分别为PA,BD上的点,且PM∶MA=BN∶ND=5∶8.
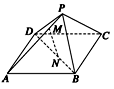
(1)求证:直线MN∥平面PBC;
(2)求线段MN的长.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年贵州黔东南州高三第二次模拟(5月)考试文科数学试卷(解析版) 题型:选择题
如图所示,正四棱锥(即底面是正方形,顶点在底面的射影是底面中心的四棱锥)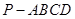 的底面面积为
的底面面积为 ,体积为
,体积为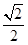 ,
,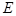 为侧棱
为侧棱 的中点,则
的中点,则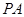 与
与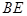 所成的角为 (
)
所成的角为 (
)
A.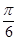 B.
B.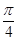 C.
C.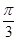 D.
D.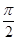
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com