
【题目】如图,我国南海某处的一个圆形海域上有四个小岛,小岛B与小岛A、小岛C相距都为5n mile,与小岛D相距为 ![]() n mile.小岛A对小岛B与D的视角为钝角,且
n mile.小岛A对小岛B与D的视角为钝角,且 ![]() .
.
(Ⅰ)求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积;
(Ⅱ)记小岛D对小岛B与C的视角为α,小岛B对小岛C与D的视角为β,求sin(2α+β)的值.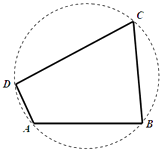
【答案】解:(Ⅰ)∵ ![]() ,且角A为钝角,∴
,且角A为钝角,∴ 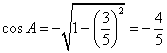 .
.
在△ABD中,由余弦定理得:AD2+AB2﹣2ADABcosA=BD2 .
∴ ![]() AD2+8AD﹣20=0.
AD2+8AD﹣20=0.
解得AD=2或AD=﹣10(舍).
∴小岛A与小岛D之间的距离为2n mile.
∵A,B,C,D四点共圆,∴角A与角C互补.
∴ ![]() ,
, ![]() .
.
在△BDC中,由余弦定理得:CD2+CB2﹣2CDCBcosC=BD2 .
∴ ![]() CD2﹣8CD﹣20=0.
CD2﹣8CD﹣20=0.
解得CD=﹣2(舍)或CD=10
∴S四边形ABCD=S△ABC+S△BCD
= ![]() =
= ![]() =3+15=18.
=3+15=18.
∴四个小岛所形成的四边形的面积为18平方n mile.
(Ⅱ)在△BDC中,由正弦定理得: ![]()
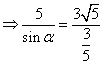
![]() .
.
∵DC2+DB2>BC2 , ∴α为锐角,∴ ![]() .
.
又∵ ![]() ,
, ![]() .
.
∴sin(2α+β)=sin[α+(α+β)]
=sinαcos(α+β)+cosαsin(α+β)=sinαcos(α+β)+cosαsin(α+β)
= ![]() =
= ![]()
【解析】(Ⅰ)利用余弦定理求出,AD,CD,即可求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积;(Ⅱ)求出sin(α+β),cos(α+β),利用和角的三角函数公式求sin(2α+β)的值.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣|x+a|
(1)当a=3时,解不等式f(x)≤ ![]() ;
;
(2)若关于x的不等式f(x)≤a解集为R,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为获得较好的收益,每年要投入一定资金用于广告促销,经调查,每年投入广告费![]() (百万元),可增加销售额约为
(百万元),可增加销售额约为![]() (百万元)(
(百万元)(![]() )
)
(1)若该公司当年的广告费控制在4百万元之内,则应该设入多少广告费,才能使该公司获得的收益最大?
(2)现该公司准备共投入6百万元,分别用于广告促销售和技术改造,经预测,每设入技术改造费![]() (百万元),可增加销售额约为
(百万元),可增加销售额约为![]() (百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益
(百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益![]() 销售额
销售额![]() 成本)
成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求f(x)+f(1﹣x)的值;
(2)若数列{an}满足an=f(0)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(1)(n∈N*),求数列{an}的通项公式;
)+f(1)(n∈N*),求数列{an}的通项公式;
(3)若数列{bn}满足bn=2nan , Sn是数列{bn}的前n项和,是否存在正实数k,使不等式knSn>3bn对于一切的n∈N*恒成立?若存在,请求出k的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,0)及圆C:x2+y2﹣6x+4y+4=0.
(1)设过P直线l1与圆C交于M、N两点,当|MN|=4时,求以MN为直径的圆Q的方程;
(2)设直线ax﹣y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】偶函数f(x)满足f(x﹣1)=f(x+1),且在x∈[0,1]时,f(x)=x2 , g(x)=ln|x|,则函数h(x)=f(x)﹣g(x)的零点的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且a2=﹣5,S5=﹣20.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求使不等式Sn>an成立的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ< ![]() )的图象与y轴的交点为(0,
)的图象与y轴的交点为(0, ![]() ),它的一个对称中心是M(
),它的一个对称中心是M( ![]() ,0),点M与最近的一条对称轴的距离是
,0),点M与最近的一条对称轴的距离是 ![]() .
.
(1)求此函数的解析式;
(2)求此函数取得最大值时x的取值集合;
(3)当x∈(0,π)时,求此函数的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com