
分析 (1)求出P的坐标,可得a,b,即可求椭圆C的方程;
(2)分类讨论,设直线l的方程为y=kx+1与椭圆C:$\frac{x^2}{4}+\frac{y^2}{3}$=1,联立消去y得(3+4k2)x2+8kx-8=0,利用根与系数关系结合$\overrightarrow{AM}$=3$\overrightarrow{MB}$,由此能求出直线l的方程.
解答 解:(1)由题意得:F(1,0),|PF|=1
∴$1+{y_0}^2=1$,∴y0=0
∴a=2,b2=3
∴椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}$=1.
(2)①当直线l的斜率不存在时,不合题意.
②当直线l的斜率存在时,设直线l的方程为y=kx+1与椭圆C:$\frac{x^2}{4}+\frac{y^2}{3}$=1联立,
消去y得(3+4k2)x2+8kx-8=0
设A(x1,y1),B(x2,y2),则${x_1}+{x_2}=-\frac{8k}{{3+4{k^2}}}$①,${x_1}{x_2}=-\frac{8}{{3+4{k^2}}}$②
∵$\overrightarrow{AM}$=3$\overrightarrow{MB}$,
∴x1=-3x2③
由①②③得${k^2}=\frac{3}{2}$,
∴$k=±\frac{{\sqrt{6}}}{2}$.
∴直线l的方程为$y=\frac{{\sqrt{6}}}{2}x+1$或$y=-\frac{{\sqrt{6}}}{2}x+1$.
点评 本题考查用待定系数法求曲线方程的能力,通过处理直线与圆锥曲线的位置关系,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想,是压轴题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2015)>f(0) | B. | f(2015)<f(0) | C. | f(2015)>e2015•f(0) | D. | f(2015)<e2015•f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
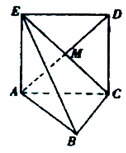 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | [2,+∞) | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com