分析:(1)设BD与AC交于O,作OK⊥AA1于K,连接DK,则DK⊥AA1,OD⊥OK,故∠DKO为二面角D-A1A-C的平面角,从而可求二面角D-A1A-C的大小.
(2)连结A1O、A1B,由于B1B∥平面A1A DD1,所以B、B1到平面A1A DD1的距离相等,由VB-A1DA=VA1-ABD,可求点B1到平面A1ADD1的距离;
(3)存在,点P在C1C的延长线上且CP=C1C,利用线面平行的判定定理,可得结论.
解答: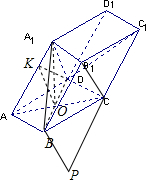
解:(1)设BD与AC交于O,作OK⊥AA
1于K,连接DK,则DK⊥AA
1,OD⊥OK,
故∠DKO为二面角D-A
1A-C的平面角,
∵∠OAK=60°,∴OK=
在菱形ABCD中,AB=2,∠ABC=60°
∴AC=AB=BC=2
∴AO=1,DO=
=
∴tan∠DKO=2,
∴二面角D-A
1A-C的平面角的余弦值是
∴二面角D-A
1A-C的大小为
arccos;
(2)连结A
1O、A
1B,由于B
1B∥平面A
1A DD
1,所以B、B
1到平面A
1A DD
1的距离相等,
设点B到平面A
1A DD
1的距离等于h.
在△AA
1O中,
A1O2=A1A2+AO2-2A1A•AOcos60°=3
∴
A1O2+AO2=A1A2∴A
1O⊥AO
而平面A A
1C
1C⊥平面ABCD,∴A
1O⊥平面ABCD
由上述第(1)问有,ED⊥A
1A
1且
ED==
∴
S△A1DA=A1A•ED=
×2×=
又
S△ABD=AO•BD=
×1×2=
由
VB-A1DA=VA1-ABD有
S△A1DA•h=S△ABD•A1O∴
h=•A1O=
×=即点B
1到平面A
1ADD
1的距离
d=(3)存在,点P在C
1C的延长线上且CP=C
1C,证明如下:
延长C
1C到P使CP=C
1C,连接B
1C,BP,则BP∥B
1C
∴BP∥A
1D
又A
1D 平面?DA
1C
1,BP?平面DA
1C
1,
∴BP∥平面DA
1C
1.
点评:本题主要考查了二面角及其度量,考查空间中直线与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于中档题.

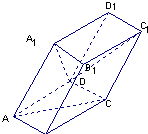 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60° 解:(1)设BD与AC交于O,作OK⊥AA1于K,连接DK,则DK⊥AA1,OD⊥OK,
解:(1)设BD与AC交于O,作OK⊥AA1于K,连接DK,则DK⊥AA1,OD⊥OK,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案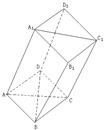 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD. 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.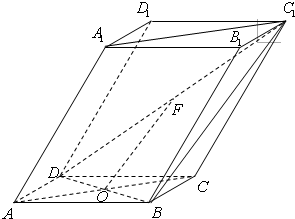 17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.
17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.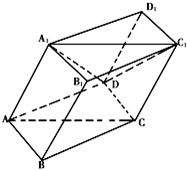 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?