
【题目】如图,已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,点
的上、下顶点,点![]() 是直线
是直线![]() 上的一个动点(与
上的一个动点(与![]() 轴的交点除外),直线
轴的交点除外),直线![]() 交椭圆于另一个点
交椭圆于另一个点![]() .
.
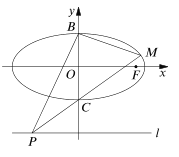
(1)当直线![]() 经过椭圆的右焦点
经过椭圆的右焦点![]() 时,求
时,求![]() 的面积;
的面积;
(2)①记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值;
为定值;
②求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)①见解析②
(2)①见解析②![]()
【解析】
试题(1)先联立直线![]() 的方程为
的方程为![]() 与椭圆方程
与椭圆方程![]() 的方程组,求出交点
的方程组,求出交点![]() 坐标
坐标![]() ,进而求出点到直线的距离公式求出上的高
,进而求出点到直线的距离公式求出上的高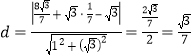 ,运用三角形的面积公式求解;(2)先求出斜率
,运用三角形的面积公式求解;(2)先求出斜率![]() 的值,再计算其积进行推算;先运用直线与椭圆的位置关系计算出向量的
的值,再计算其积进行推算;先运用直线与椭圆的位置关系计算出向量的![]() 的坐标形式,再运用向量的数量积公式进行推证:
的坐标形式,再运用向量的数量积公式进行推证:
解:(1)由题意![]() ,焦点
,焦点![]() ,
,
当直线![]() 过椭圆的右焦点
过椭圆的右焦点![]() 时,则直线
时,则直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
联立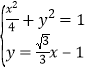 ,解得
,解得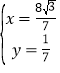 或
或![]() (舍),即
(舍),即![]() .
.
连![]() ,则直线
,则直线![]() ,即
,即 ![]() ,
,
而![]() ,
,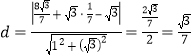 .
.
故![]() .
.
(2)解:法一:①设![]() ,且
,且![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
联立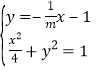 化简得
化简得![]() ,
,
解得![]() ,
,
所以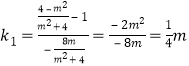 ,
,![]() ,
,
所以![]() 为定值.
为定值.
②由①知,![]() ,
,![]() ,
,
所以![]() ,
,
令![]()
故![]() ,
,
因为![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
解法二:①设点![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() .
.
所以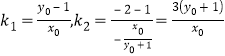 ,
,
所以![]() (定值).
(定值).
②由①知,![]() ,
,![]() ,
,
所以,![]()
![]() .
.
令![]() ,则
,则![]() ,
,
因为![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a,b,c,cos2C+2 ![]() cosC+2=0.
cosC+2=0.
(1)求角C的大小;
(2)若b= ![]() a,△ABC的面积为
a,△ABC的面积为 ![]() sinAsinB,求sinA及c的值.
sinAsinB,求sinA及c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍,右焦点为
倍,右焦点为![]() ,点
,点![]() 分别是该椭圆的上、下顶点,点
分别是该椭圆的上、下顶点,点![]() 是直线
是直线![]() 上的一个动点(与
上的一个动点(与![]() 轴交点除外),直线
轴交点除外),直线![]() 交椭圆于另一点
交椭圆于另一点![]() ,记直线
,记直线![]() ,
, ![]() 的斜率分别为
的斜率分别为![]()

(1)当直线![]() 过点
过点![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上单调函数,且对x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,则方程f(x)﹣f′(x)=e的实数解所在的区间是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(1,e)
D.(e,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=4,AB=4 ![]() ,∠CDA=120°,点N在线段PB上,且PN=2.
,∠CDA=120°,点N在线段PB上,且PN=2. 
(1)求证:BD⊥PC;
(2)求证:MN∥平面PDC;
(3)求二面角A﹣PC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
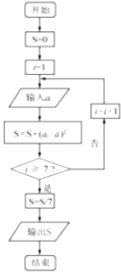
【题目】某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中 ![]() 是这7个数据的平均数),则输出的S的值是( )
是这7个数据的平均数),则输出的S的值是( )
观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABC﹣A1B1C1中,点D是BC的中点. 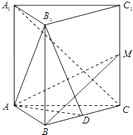
(1)求证:A1C∥平面AB1D;
(2)设M为棱CC1的点,且满足BM⊥B1D,求证:平面AB1D⊥平面ABM.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com