
【题目】在平面直角坐标系xoy中,已知圆C1:(x+3)2+(y﹣1)2=4和圆C2:(x﹣4)2+(y﹣5)2=4
(1)若直线l过点A(4,0),且被圆C1截得的弦长为2 ![]() ,求直线l的方程
,求直线l的方程
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线l1和l2 , 它们分别与圆C1和C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,求所有满足条件的点P的坐标.
【答案】
(1)解:由于直线x=4与圆C1不相交;
∴直线l的斜率存在,设l方程为:y=k(x﹣4)
圆C1的圆心到直线l的距离为d,∵l被⊙C1截得的弦长为2 ![]()
∴d= ![]() =1
=1
d= ![]() 从而k(24k+7)=0即k=0或k=﹣
从而k(24k+7)=0即k=0或k=﹣ ![]()
∴直线l的方程为:y=0或7x+24y﹣28=0
(2)解:设点P(a,b)满足条件,
由题意分析可得直线l1、l2的斜率均存在且不为0,
不妨设直线l1的方程为y﹣b=k(x﹣a),k≠0
则直线l2方程为:y﹣b=﹣ ![]() (x﹣a)
(x﹣a)
∵⊙C1和⊙C2的半径相等,及直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,
∴⊙C1的圆心到直线l1的距离和圆C2的圆心到直线l2的距离相等
即 ![]() =
= 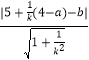
整理得|1+3k+ak﹣b|=|5k+4﹣a﹣bk|
∴1+3k+ak﹣b=±(5k+4﹣a﹣bk)即(a+b﹣2)k=b﹣a+3或(a﹣b+8)k=a+b﹣5
因k的取值有无穷多个,所以 ![]() 或
或 ![]()
解得 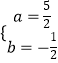 或
或 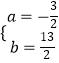
这样的点只可能是点P1( ![]() ,﹣
,﹣ ![]() )或点P2(﹣
)或点P2(﹣ ![]() ,
, ![]() )
)
【解析】(1)因为直线l过点A(4,0),故可以设出直线l的点斜式方程,又由直线被圆C1截得的弦长为2 ![]() ,根据半弦长、半径、弦心距满足勾股定理,我们可以求出弦心距,即圆心到直线的距离,得到一个关于直线斜率k的方程,解方程求出k值,代入即得直线l的方程.(2)与(1)相同,我们可以设出过P点的直线l1与l2的点斜式方程,由于两直线斜率为1,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,故我们可以得到一个关于直线斜率k的方程,解方程求出k值,代入即得直线l1与l2的方程.
,根据半弦长、半径、弦心距满足勾股定理,我们可以求出弦心距,即圆心到直线的距离,得到一个关于直线斜率k的方程,解方程求出k值,代入即得直线l的方程.(2)与(1)相同,我们可以设出过P点的直线l1与l2的点斜式方程,由于两直线斜率为1,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,故我们可以得到一个关于直线斜率k的方程,解方程求出k值,代入即得直线l1与l2的方程.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图中的信息,回答下列问题: 
(Ⅰ)补全频率分布直方图;
(Ⅱ)估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)用分层抽样的方法在分数段为[110,130)的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(Ⅰ)证明:A=2B
(Ⅱ)若△ABC的面积S= ![]() ,求角A的大小.
,求角A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设入射光线沿直线y=2x+1射向直线y=x,则被y=x反射后,反射光线所在的直线方程是( )
A.x﹣2y﹣1=0
B.x﹣2y+1=0
C.3x﹣2y+1=0
D.x+2y+3=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对新研发的一种产品进行合理定价,且销量与单价具有相关关系,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(单位:元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(单位:万件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)现有三条y对x的回归直线方程: ![]() =﹣10x+170;
=﹣10x+170; ![]() =﹣20x+250;
=﹣20x+250; ![]() =﹣15x+210;根据所学的统计学知识,选择一条合理的回归直线,并说明理由.
=﹣15x+210;根据所学的统计学知识,选择一条合理的回归直线,并说明理由.
(2)预计在今后的销售中,销量与单价服从(1)中选出的回归直线方程,且该产品的成本是每件5元,为使公司获得最大利润,该产品的单价应定多少元?(利润=销售收入﹣成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数: 907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,这三天中恰有两天下雨的概率近似为( )
A.0.35
B.0.25
C.0.20
D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次,记录如下:
甲 | 88 | 89 | 92 | 90 | 91 |
乙 | 84 | 88 | 96 | 89 | 93 |
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?请说明理由.(用样本数据特征来说明.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)判断函数![]() 在
在![]() 内零点的个数,并说明理由;
内零点的个数,并说明理由;
(Ⅱ)![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,记过点
,记过点![]() 的直线的斜率为
的直线的斜率为![]() ,问:是否存在实数
,问:是否存在实数![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com