
有下列命题:
①设集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必要条件;
②命题:“若a∈M,则b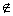 M”的逆否命题是:若b∈M,则a
M”的逆否命题是:若b∈M,则a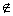 M;
M;
③若p∧q是假命题,则p、q都是假命题;
④命题P:“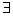 x0∈R,x
x0∈R,x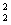 -x0-1>0”的否定
-x0-1>0”的否定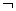 P:“
P:“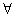 x∈R,x2-x-1≤0”.
x∈R,x2-x-1≤0”.
其中真命题的序号是________.
②④
解析试题分析:本题考查的知识点是,判断命题真假.(1)考查了集合间的关系,在集合M中任取一个x值,看其是否在集合N中,反之,在集合N中任取一个x值,判断其是否又在集合M中;(2)考查命题的逆否命题,把原命题的结论取否定作为条件,条件取否定作为结论;(3)考查复合命题的真假判断,两个命题中只要有一个假命题,则p∧q为假命题;(4)考查特称命题的否定,注意特称命题的否定全称命题的格式.解:对于①,a在集合M中取值为3,但3不在集合N中,有a∈M,但a∉N,所以“a∈M”是“a∈N”的不充分条件,所以①不正确;对于②,把原命题的结论取否定作为条件,条件取否定作为结论,所以,命题“若a∈M,则b∉M”的逆否命题是:若b∈M,则a∉M,所以命题②正确;
对于③,假若p,q中有一个为真命题,则p∧q也是假命题,所以,命题③不正确;对于④,特称命题的否定是全称命题,所以命题P:“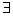 x0∈R,x
x0∈R,x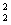 -x0-1>0”的否定¬P:“?x∈R,x2-x-1≤0”正确正确,故②④
-x0-1>0”的否定¬P:“?x∈R,x2-x-1≤0”正确正确,故②④
考点:命题的真假判断
点评:本题考查了命题的真假判断与运用,解答的关键是熟练基本概念,掌握有关格式,如特称命题否定的格式 特称命题P:?x0∈M,p(x0),否定¬p:?x∈M,¬p(x).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
下列结论中是真命题的是__________(填序号).
①f(x)=ax2+bx+c在[0,+∞)上是增函数的一个充分条件是-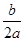 <0;
<0;
②已知甲:x+y≠3,乙:x≠1或y≠2,则甲是乙的充分不必要条件;
③数列{an}(n∈N*)是等差数列的充要条件是Pn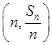 是共线的.
是共线的.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知命题 :“函数
:“函数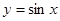 是周期函数且是奇函数”,则
是周期函数且是奇函数”,则
①命题 是“
是“ ”命题; ②命题
”命题; ②命题 是真命题;
是真命题;
③命题非 :函数
:函数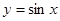 不是周期函数且不是奇函数;
不是周期函数且不是奇函数;
④命题非 是假命题.其中,正确叙述的个数是
是假命题.其中,正确叙述的个数是
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列四个命题:
①在 中,若
中,若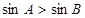 ,则
,则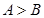 ;
;
②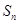 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,则
,则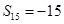 ;
;
③数列 的前n项和为
的前n项和为 且满足
且满足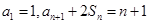 ,则
,则
④数列 满足
满足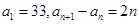 ,则
,则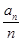 的最小值为
的最小值为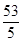
其中正确的命题序号 (注:把你认为正确的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com