
【题目】如图,某人在塔的正东方向上的![]() 处在与塔垂直的水平面内沿南偏西
处在与塔垂直的水平面内沿南偏西![]() 的方向以每小时
的方向以每小时![]() 千米的速度步行了
千米的速度步行了![]() 分钟以后,在点
分钟以后,在点![]() 处望见塔的底端
处望见塔的底端![]() 在东北方向上,已知沿途塔的仰角
在东北方向上,已知沿途塔的仰角![]() ,
,![]() 的最大值为
的最大值为![]() .
.
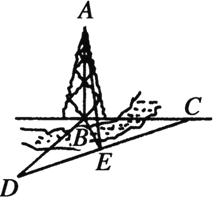
(1)求该人沿南偏西![]() 的方向走到仰角
的方向走到仰角![]() 最大时,走了几分钟;
最大时,走了几分钟;
(2)求塔的高![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
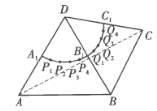
【题目】如图,正四面体![]() 的各棱长均为2,
的各棱长均为2,![]() 、
、![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 、
、![]() 的中点,以
的中点,以![]() 为圆心、1为半径,分别在面
为圆心、1为半径,分别在面![]() 、面
、面![]() 内作弧
内作弧![]() ,并将两弧各分成五等份,分点顺次为
,并将两弧各分成五等份,分点顺次为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 以及
以及![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .一只甲虫欲从点
.一只甲虫欲从点![]() 出发,沿四面体表面爬行至点
出发,沿四面体表面爬行至点![]() ,则其爬行的最短距离为___________。
,则其爬行的最短距离为___________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,a1+2a2+3a3+…+nan=![]() (n∈N*)
(n∈N*)
(Ⅰ)证明当n≥2时,数列{nan}是等比数列,并求数列{an}的通项an;
(Ⅱ)求数列{n2an}的前n项和Tn;
(Ⅲ)对任意n∈N*,使得![]() 恒成立,求实数λ的最小值.
恒成立,求实数λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园内有一块以![]() 为圆心半径为
为圆心半径为![]() 米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形
米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形![]() 区域,其中两个端点
区域,其中两个端点![]() ,
,![]() 分别在圆周上;观众席为梯形
分别在圆周上;观众席为梯形![]() 内切在圆
内切在圆![]() 外的区域,其中
外的区域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在点
在点![]() 的同侧.为保证视听效果,要求观众席内每一个观众到舞台
的同侧.为保证视听效果,要求观众席内每一个观众到舞台![]() 处的距离都不超过
处的距离都不超过![]() 米.设
米.设![]() ,
,![]() .问:对于任意
.问:对于任意![]() ,上述设计方案是否均能符合要求?
,上述设计方案是否均能符合要求?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给图中A,B,C,D,E,F六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有4种颜色可供选择,则共有___种不同的染色方案.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程选讲.
:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]()
![]() (
(![]() 为参数,实数
为参数,实数![]() ). 在以
). 在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点. 当
两点. 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com