
【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如下柱状图:

(1)从样本中任意选取2名学生,求恰好有一名学生的打分不低于4分的概率;
(2)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记![]() 表示两人打分之和,求
表示两人打分之和,求![]() 的分布列和
的分布列和![]() .
.
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是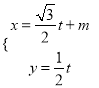 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆![]() 的参数方程为
的参数方程为 (
(![]() 为参数),若
为参数),若![]() 是圆
是圆![]() 与
与![]() 轴正半轴的交点,以坐标原点
轴正半轴的交点,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,设过点
轴正半轴为极轴,建立极坐标系,设过点![]() 的圆
的圆![]() 的切线为
的切线为![]() .
.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)求圆![]() 上到直线
上到直线![]() 的距离最大的点的直角坐标.
的距离最大的点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
![]() 的浓度;
的浓度;
(ii)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
参考公式:回归直线的方程是![]() ,其中
,其中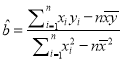 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装![]() 台发电机的水电站,过去
台发电机的水电站,过去![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足![]() 的年份有
的年份有![]() 年,不低于
年,不低于![]() 且不超过
且不超过![]() 的年份有
的年份有![]() 年,超过
年,超过![]() 的年份有
的年份有![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来![]() 年中,设
年中,设![]() 表示流量超过
表示流量超过![]() 的年数,求
的年数,求![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 |
|
|
|
若某台发电机运行,则该台年利润为![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是 ( )
A. 某校高三(1)班有55人,2班有54人,3班有52人,由此得高三所有班人数超过50人
B. 两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180°
C. 由平面三角形的性质,推测空间四边形的性质
D. 在数列{an}中,a1=1,an=![]() (an-1+
(an-1+![]() )(n≥2),由此归纳出{an}的通项公
)(n≥2),由此归纳出{an}的通项公
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com