Question

设函数f（x）=x²-2|x|-3（-3≤x≤3），
（1）证明函数f（x）是偶函数；
（2）用分段函数表示f（x）并作出其图象；
（3）指出函数f（x）的单调区间及相应的单调性；
（4）求函数的值域．

Answer 1

分析：（1）根据函数奇偶性的定义，我们先判断函数的定义域是否关于原点对称，然后再判断f（-x）与f（x）的关系，若f（-x）与f（x）相等则函数f（x）是偶函数；
（2）由于函数的解析式中，含有绝对值符合，我们可以用零点分段法，即分0≤x≤3主-3≤x＜0两种情况，进行分类讨论，易得函数的解析式，然后根据分段函数的图象分段画的原则，易得到函数的图象．
（3）由函数图象，根据图象上升，函数递增，图象下降，函数递减的原则，确定函数的单调区间；
（4）由函数图象，易得到函数最高点，最低点坐标，进而得到函数的值域．

解答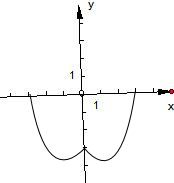：解：（1）∵-3≤x≤3，
∴函数的定义域关于原点对称，
又∵f（-x）=（-x）²-2|-x|-3=x²-2|x|-3=f（x）
∴函数f（x）是偶函数．
（2）f（x）=

x2-2x-3，0≤x≤3 x2+2x-3，-3≤x＜0

；
（3）由（2）中图象可得：
函数f（x）的单调增区间是[-1，0]，[1，3]；
函数f（x）的单调减区间是[-3，-1]，[0，1]．
（4）由（2）中图象可得：
函数的值域是[-4，0]．

点评：本题考查的知识点是函数的图象，函数的单调性及单调区间，及函数的奇偶性的判断，利用零点分段法将函数的解析式化为分段函数，并画出函数的图象是解答本题的关键．