
分析 以AB中点为坐标原点,建立如图所示的直角坐标系,可得A(-1,0),B(1,0),C(0,$\sqrt{3}$),讨论P在AB,BC,CA上,分别设P的坐标,可得向量PA,PB,PC的坐标,由向量的坐标表示,化为二次函数在闭区间上的最值问题,即可得到所求取值范围.
解答 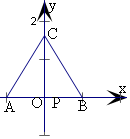 解:以AB中点为坐标原点,建立如图所示的直角坐标系,
解:以AB中点为坐标原点,建立如图所示的直角坐标系,
可得A(-1,0),B(1,0),C(0,$\sqrt{3}$),
当P在线段AB上,设P(t,0),(-1≤t≤1),
$\overrightarrow{PA}$=(-1-t,0),$\overrightarrow{PB}$=(1-t,0),$\overrightarrow{PC}$=(-t,$\sqrt{3}$),
即有$\overrightarrow{PA}$•($\overrightarrow{PB}$+$\overrightarrow{PC}$)=(-1-t,0)•(1-2t,$\sqrt{3}$)
=(-1-t)(1-2t)+0×$\sqrt{3}$=2t2+t-1=2(t-$\frac{1}{4}$)2-$\frac{9}{8}$,
由-1≤t≤1可得t=$\frac{1}{4}$取得最小值-$\frac{9}{8}$,t=-1时,取得最大值0;
当P在线段CB上,设P(m,$\sqrt{3}$(1-m)),(0≤m≤1),
$\overrightarrow{PA}$=(-1-m,$\sqrt{3}$(m-1)),$\overrightarrow{PB}$=(1-m,$\sqrt{3}$(m-1)),$\overrightarrow{PC}$=(-m,$\sqrt{3}$m),
即有$\overrightarrow{PA}$•($\overrightarrow{PB}$+$\overrightarrow{PC}$)=(-1-m,$\sqrt{3}$(m-1))•(1-2m,$\sqrt{3}$(2m-1))
=(-1-m)(1-2m)+$\sqrt{3}$(m-1)×$\sqrt{3}$(2m-1)=2(2m-1)2,
由0≤m≤1可得m=$\frac{1}{2}$取得最小值0,m=0或1时,取得最大值2;
当P在线段AC上,设P(n,$\sqrt{3}$(1+n)),(-1≤n≤0),
$\overrightarrow{PA}$=(-1-n,-$\sqrt{3}$(1+n)),$\overrightarrow{PB}$=(1-n,-$\sqrt{3}$(1+n)),$\overrightarrow{PC}$=(-n,-$\sqrt{3}$n),
即有$\overrightarrow{PA}$•($\overrightarrow{PB}$+$\overrightarrow{PC}$)=(-1-n,-$\sqrt{3}$(1+n))•(1-2n,-$\sqrt{3}$(1+2n))
=(-1-n)(1-2n)+$\sqrt{3}$(1+n)×$\sqrt{3}$(1+2n)=8n2+10n+2=8(n+$\frac{5}{8}$)2-$\frac{9}{8}$,
由-1≤n≤0可得n=-$\frac{5}{8}$取得最小值-$\frac{9}{8}$,n=0时,取得最大值2;
综上可得$\overrightarrow{PA}$•($\overrightarrow{PB}$+$\overrightarrow{PC}$)的取值范围是[-$\frac{9}{8}$,2].
故答案为:[-$\frac{9}{8}$,2].
点评 本题考查向量数量积的坐标表示,考查坐标法的运用,同时考查分类讨论和转化思想,转化为二次函数在闭区间上的最值问题是解题的关键,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | 6 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在区间(-1,0)内没有实数根 | |
| B. | 在区间(-1,0)内有一个实数根,在(-1,0)外有一个实数根 | |
| C. | 在区间(-1,0)内有两个相等的实数根 | |
| D. | 在区间(-1,0)内有两个不相等的实数根 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年陕西省高一下学期期末考数学试卷(解析版) 题型:解答题
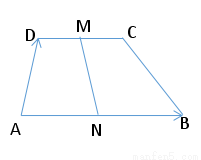
如图,ABCD是一个梯形,AB∥CD,且AB=2CD,M、N分别是DC、AB的中点,已知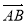 =a,
=a,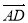 =b,试用a、b分别表示
=b,试用a、b分别表示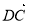 、
、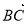 、
、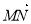 .
.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年陕西省高一下学期期末考数学试卷(解析版) 题型:选择题
为了得到函数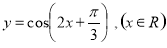 的图像,只需把函数
的图像,只需把函数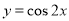 的图像
的图像
A.向左平行移动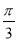 个单位
个单位
B.向右平行移动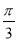 个单位
个单位
C.向左平行移动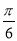 个单位
个单位
D.向右平行移动个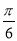 单位
单位
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com