
����Ŀ��Ϊ�˵���ij����ӻ����������о���Ա�Ըÿ���ӻ���������Ӧ�IJ��ԣ����õ������ݷ��飺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����ͳ����ͼ��ʾ��
����ͳ����ͼ��ʾ��
���Բ�ͬ�Ա������������ӻ��Ĺ�����Ը�������飬�õ����������±���ʾ��
Ը���ÿ���ӻ� | ��Ը���ÿ���ӻ� | �ܼ� | |
���� | 800 | 1000 | |
�� | 600 | ||
�ܼ� | 1200 |
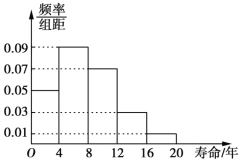
��1������ͼ�е����ݣ��Թ��Ƹÿ���ӻ���ƽ��������
��2�����ݱ������ݣ��ܷ��ڷ�����ĸ��ʲ�����0.001��ǰ������Ϊ���Ƿ�Ը���ÿ���ӻ����롰������Ա��йأ�
��3����Ƶ�ʹ��Ƹ��ʣ����ڸÿ���ӻ����������������ȡ4̨������������������4��ĵ��ӻ���̨��ΪX����X�ķֲ��м���ѧ����.
�ο���ʽ�����ݣ�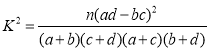 ������
������![]() ��
��
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
���𰸡���1���ÿ���ӻ���ƽ������ԼΪ7.76�ꣻ ��2���ڷ�����ĸ��ʲ�����0.001��ǰ������Ϊ���Ƿ�Ը���ÿ���ӻ�������������Ա����й�.�� ��3��![]() .
.
��������
��1������Ƶ�ʷֲ�ֱ��ͼ����������ݵ�Ƶ�ʣ����ø����Ƶ�ʳ��Ը������ݵ��м�ֵ����ͼ��õ�ƽ������
��2�������Ʊ������ݣ��ɱ������ݼ���![]() �Ĺ۲�ֵ���ٽ����жϡ�
�Ĺ۲�ֵ���ٽ����жϡ�
��3����Ƶ�ʷֲ�ֱ��ͼ��֪���ӻ���������������ĸ���Ϊ![]() ���г��ֲ�������������
���г��ֲ�������������
��1��![]()
![]() ��
��
�ʸÿ���ӻ���ƽ������ԼΪ7.76��.
��2�������⣬���Ʊ��е��������±���ʾ��
Ը���ÿ���ӻ� | ��Ը���ÿ���ӻ� | �ܼ� | |
���� | 800 | 200 | 1000 |
�� | 400 | 600 | 1000 |
�ܼ� | 1200 | 800 | 2000 |
�����![]() �Ĺ۲�ֵΪ
�Ĺ۲�ֵΪ![]() .
.
�����ڷ�����ĸ��ʲ�����0.001��ǰ������Ϊ���Ƿ�Ը���ÿ���ӻ�������������Ա����й�.
��3�������⣬![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() .
.
��X�ķֲ���Ϊ
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
![]() .
.


 ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ʵ����
��ʵ����![]() �����
�����![]() ����
Ϊ����![]() ��һ��������.��֪����
��һ��������.��֪����![]() ��
��![]() ��.
��.
��1����![]() ����֤��
����֤��![]() ��Ψһ�����㣻
��Ψһ�����㣻
��2����![]() �����������㣬��ʵ��a��ȡֵ��Χ.
�����������㣬��ʵ��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Ϊ3���߶�![]() �����˵�
�����˵�![]() ��
��![]() �ֱ���
�ֱ���![]() ���
���![]() �����ƶ���
�����ƶ���![]() .
.
��1�����![]() �Ĺ켣
�Ĺ켣![]() �ķ���.
�ķ���.
��2����![]() �����ഹֱ������ֱ�߷ֱ���켣
�����ഹֱ������ֱ�߷ֱ���켣![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �е�Ϊ
�е�Ϊ![]() ��
��![]() �е�Ϊ
�е�Ϊ![]() ����̽��ֱ��
����̽��ֱ��![]() �Ƿ�����㣿���ǣ�����ö��㣻�����ǣ�˵������.
�Ƿ�����㣿���ǣ�����ö��㣻�����ǣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ,����
,����![]()
��1����![]() ʱ,������
ʱ,������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2��������![]() ������Сֵ
������Сֵ![]() ,��֤:
,��֤:![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�����
�У�����![]() �������Σ�
��������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ�����
�ֱ�����![]() ��
��![]() ��
��![]() ���е㣬����ƽ��
���е㣬����ƽ��![]() ������
������![]() ���õĽ������Σ��������������ۣ�
���õĽ������Σ��������������ۣ�
�ٽ�����������![]() ��
��
�ڽ�����һ������Σ�
�۽���ֻ������![]() ���������е������ཻ��
���������е������ཻ��
���У�������ȷ���۵������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��һ���߶��꼶��ȫ��ѧ�����μ������ʽ������ԣ����Գɼ�����Ϊ100�֣��涨���Գɼ���![]() ֮��Ϊ���������㡱����
֮��Ϊ���������㡱����![]() ֮��Ϊ���������á�����
֮��Ϊ���������á�����![]() ֮��Ϊ�����ʺϸ���
֮��Ϊ�����ʺϸ���![]() ֮��Ϊ�����ʲ��ϸ�.�ִ��������꼶�и������ȡ7��ѧ�������Գɼ����£�
֮��Ϊ�����ʲ��ϸ�.�ִ��������꼶�и������ȡ7��ѧ�������Գɼ����£�

����m��n��������.
��������У��һ�꼶��280ѧ�����Թ��Ƹ�һ�꼶���������㡱��ѧ��������
�������Ӹ�һ�꼶��ȡ��7��ѧ���������ȡ2�ˣ���XΪ��ȡ��2����Ϊ���������á���ѧ����������X�ķֲ��м���ѧ������
�����������꼶����ȡѧ���IJ��Գɼ���ƽ������ȣ����߶��꼶����ȡѧ���IJ��Գɼ��ķ�����Сʱ��д��m��n��ֵ.��ֻ��д�����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ������
������![]() �Ҳ�����
�Ҳ�����![]() ��ֱ������Բ
��ֱ������Բ![]() ����
����![]() ��
��![]() ���㣬ֱ��
���㣬ֱ��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ��
��
������![]() ��ֱ��
��ֱ��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() ��б�ʣ�
��б�ʣ�
�������ж�ֱ��![]() ��ֱ��
��ֱ��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)��log4(4x��1)��kx(k��R)��ż������
(1)��k��ֵ��
(2)��g(x)��log4![]() ��������f(x)��g(x)��ͼ������ֻ��һ�������㣬��ʵ��a��ȡֵ��Χ��
��������f(x)��g(x)��ͼ������ֻ��һ�������㣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
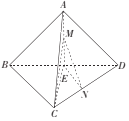
����Ŀ����ͼ��������A��BCD�У���E��BD�ϣ�EA��EB��EC��ED��BD![]() CD����ACDΪ�������Σ���M��N�ֱ���AE��CD���˶��������˵㣩����AM��CN����������C��EMN�����ȡ�����ֵ
CD����ACDΪ�������Σ���M��N�ֱ���AE��CD���˶��������˵㣩����AM��CN����������C��EMN�����ȡ�����ֵ![]() ʱ������A��BCD�������ı����Ϊ_____.
ʱ������A��BCD�������ı����Ϊ_____.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com