
【题目】如图,射线![]() 和
和![]() 均为笔直的公路,扇形
均为笔直的公路,扇形![]() 区域(含边界)是规划的生态文旅园区,其中
区域(含边界)是规划的生态文旅园区,其中![]() 、
、![]() 分别在射线
分别在射线![]() 和
和![]() 上.经测量得,扇形
上.经测量得,扇形![]() 的圆心角(即
的圆心角(即![]() )为
)为![]() 、半径为
、半径为![]() 千米.根据发展规划,要在扇形
千米.根据发展规划,要在扇形![]() 区域外修建一条公路
区域外修建一条公路![]() ,分别与射线
,分别与射线![]() 、
、![]() 交于
交于![]() 、
、![]() 两点,并要求
两点,并要求![]() 与扇形弧
与扇形弧![]() 相切于点
相切于点![]() (
(![]() 不与
不与![]() 重合).设
重合).设![]() (单位:弧度),假设所有公路的宽度均忽略不计.
(单位:弧度),假设所有公路的宽度均忽略不计.
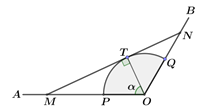
(1)试将公路![]() 的长度表示为
的长度表示为![]() 的函数;
的函数;
(2)已知公路每千米的造价为![]() 万元,问建造这样一条公路
万元,问建造这样一条公路![]() ,至少要投入多少万元?
,至少要投入多少万元?
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,
,![]() .
.
(1)若直线![]() ,
,![]() 分别经过定点
分别经过定点![]() ,
,![]() ,求定点
,求定点![]() ,
,![]() 的坐标;
的坐标;
(2)是否存在一个定点![]() ,使得
,使得![]() 与
与![]() 的交点到定点
的交点到定点![]() 的距离为定值?如果存在,求出定点
的距离为定值?如果存在,求出定点![]() 的坐标及定值
的坐标及定值![]() ;如果不存在,说明理由.
;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,
中,![]() 和
和![]() 交于一点,除
交于一点,除![]() 以外的其余各棱长均为2.
以外的其余各棱长均为2.
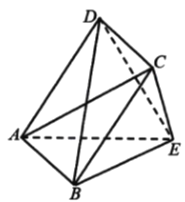
![]() 作平面
作平面![]() 与平面
与平面![]() 的交线
的交线![]() ,并写出作法及理由;
,并写出作法及理由;
![]() 求证:平面
求证:平面![]() 平面
平面![]() ;
;
![]() 若多面体的体积为2,求直线
若多面体的体积为2,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象相邻两条对称轴之间的距离为
图象相邻两条对称轴之间的距离为![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到的图象关于
个单位,得到的图象关于![]() 轴对称,则( )
轴对称,则( )
A. 函数![]() 的周期为
的周期为![]() B. 函数
B. 函数![]() 图象关于点
图象关于点![]() 对称
对称
C. 函数![]() 图象关于直线
图象关于直线![]() 对称 D. 函数
对称 D. 函数![]() 在
在![]() 上单调
上单调
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com