
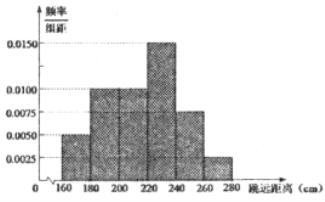
【题目】某校为了解高三男生的体能达标情况,抽调了120名男生进行立定跳远测试,根据统计数据得到如下的频率分布直方图.若立定跳远成绩落在区间![]() 的左侧,则认为该学生属“体能不达标的学生,其中
的左侧,则认为该学生属“体能不达标的学生,其中![]() 分别为样本平均数和样本标准差,计算可得
分别为样本平均数和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
(1)若该校高三某男生的跳远距离为![]() ,试判断该男生是否属于“体能不达标”的学生?
,试判断该男生是否属于“体能不达标”的学生?
(2)该校利用分层抽样的方法从样本区间![]() 中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在
中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在![]() 的概率.
的概率.
【答案】(1)该生属于“体能不达标”的学生(2)![]()
【解析】
(1)由题可知,根据频率=纵坐标×组距,分别求出各组频率=各组小矩形面积,便可频率分布直方图的平均数![]() ,即可判断;
,即可判断;
(2)由频数=频率×样本容量,可求出![]() 对应的人数,再按分层抽样抽取5人,分别抽出1人,2人,2人,再从5人中抽2人,最后用一一列举出来,用古典概型即可求出答案.
对应的人数,再按分层抽样抽取5人,分别抽出1人,2人,2人,再从5人中抽2人,最后用一一列举出来,用古典概型即可求出答案.
(1)由题意可知:各小矩形面积从左至右依次为0.1,0.2,0.2,0.3,0.15,0.05
![]()
![]() ∵
∵![]() ∴该生属于“体能不达标”的学生
∴该生属于“体能不达标”的学生
(2)由题意,跳远距离在![]() 的人数分别为12人、24人、24人
的人数分别为12人、24人、24人
按分层抽样抽取5人,则![]() 抽1人,
抽1人,![]() 抽2人,
抽2人,![]() 抽2人
抽2人
设![]() 抽出的人编号为
抽出的人编号为![]() ,
,![]() 抽出的人编号为
抽出的人编号为![]() ,
,
![]() 抽出的人编号为
抽出的人编号为![]()
从中选两人,![]() ,共有10种情况
,共有10种情况
记选出的两人中恰有一人跳远距离在![]() 为事件
为事件![]() ,满足条件的基本事件有6种,分别为
,满足条件的基本事件有6种,分别为![]()
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,动圆
,动圆![]() 与圆
与圆![]() 和圆
和圆![]() 均内切.
均内切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 且垂直于
且垂直于![]() 的直线交轨迹
的直线交轨迹![]() 于两点
于两点![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是全球最大的口罩生产国,在2020年3月份,我国每日口罩产量超一亿只,已基本满足国内人民的需求,但随着疫情在全球范围扩散,境外口罩需求量激增,世界卫生组织公开呼吁扩大口罩产能常见的口罩有![]() 和
和![]() (分别阻挡不少于90.0%和95.0%的0.055到0.095微米的氯化钠颗粒)两种,某口罩厂两条独立的生产线分别生产
(分别阻挡不少于90.0%和95.0%的0.055到0.095微米的氯化钠颗粒)两种,某口罩厂两条独立的生产线分别生产![]() 和
和![]() 两种口罩,为保证质量对其进行多项检测并评分(满分100分),规定总分大于或等于85分为合格,小于85分为次品,现从流水线上随机抽取这两种口罩各100个进行检测并评分,结果如下:
两种口罩,为保证质量对其进行多项检测并评分(满分100分),规定总分大于或等于85分为合格,小于85分为次品,现从流水线上随机抽取这两种口罩各100个进行检测并评分,结果如下:
总分 |
|
|
|
|
|
| 6 | 14 | 42 | 31 | 7 |
| 4 | 6 | 47 | 35 | 8 |
(1)试分别估计两种口罩的合格率;
(2)假设生产一个![]() 口罩,若质量合格,则盈利3元,若为次品则亏损1元;生产一个
口罩,若质量合格,则盈利3元,若为次品则亏损1元;生产一个![]() 口罩,若质量合格,则盈利8元,若为次品则亏损2元,在(1)的前提下,
口罩,若质量合格,则盈利8元,若为次品则亏损2元,在(1)的前提下,
①设![]() 为生产一个
为生产一个![]() 口罩和生产一个
口罩和生产一个![]() 口罩所得利润的和,求随机变量
口罩所得利润的和,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
②求生产4个![]() 口罩所得的利润不少于8元的概率
口罩所得的利润不少于8元的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在![]() 内的概率;
内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情后,为了支持企业复工复产,某地政府决定向当地企业发放补助款,其中对纳税额在![]() 万元至
万元至![]() 万元(包括
万元(包括![]() 万元和
万元和![]() 万元)的小微企业做统一方案.方案要求同时具备下列两个条件:①补助款
万元)的小微企业做统一方案.方案要求同时具备下列两个条件:①补助款![]() (万元)随企业原纳税额
(万元)随企业原纳税额![]() (万元)的增加而增加;②补助款不低于原纳税额
(万元)的增加而增加;②补助款不低于原纳税额![]() (万元)的
(万元)的![]() .经测算政府决定采用函数模型
.经测算政府决定采用函数模型![]() (其中
(其中![]() 为参数)作为补助款发放方案.
为参数)作为补助款发放方案.
(1)判断使用参数![]() 是否满足条件,并说明理由;
是否满足条件,并说明理由;
(2)求同时满足条件①、②的参数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试研究,一个三角形能否同时具有以下两个性质:(1)三边是连续的三个自然数;(2)最大角是最小角的2倍.若能,请求出这个三角形的三边以及最大角的余弦值;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB//DC,AB=2CD,∠BCD=90°.
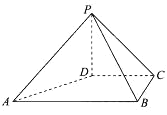
(1)求证:AD⊥PB;
(2)求点C到平面PAB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用电范围(度) | (0,210] | (210,400] |
|
某市随机抽取10户同一个月的用电情况,得到统计表如下:
居民用电户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用电量(度) | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯的部分每度0.8元,试计算A居民用电户用电410度时应电费多少元?
现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
以表中抽到的10户作为样本估计全市的居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com