
【题目】某企业对设备进行技术升级改造,为了检验改造效果,现从设备改造后生产的大量产品中抽取了100件产品作为样本,检测一项质量指标值,统计整理为如图所示的频率分布直方图:
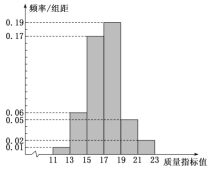
(1)估计该企业所生产产品的质量指标的平均数和中位数(中位数保留一位小数);
(2)若产品的质量指标在![]() 内,则该产品为残次品,生产并销售一件残次品该企业损失1万元;若产品的质量指标在
内,则该产品为残次品,生产并销售一件残次品该企业损失1万元;若产品的质量指标在![]() 范围内,则该产品为特优品,生产一件特优品该企业获利3万元.把样本中的残次品和特优品取出合并在一起,在从中任取2件产品进行销售,那么该企业收入为多少万元的可能性最大?
范围内,则该产品为特优品,生产一件特优品该企业获利3万元.把样本中的残次品和特优品取出合并在一起,在从中任取2件产品进行销售,那么该企业收入为多少万元的可能性最大?
【答案】(1)17.08,17.1;(2)2万元.
【解析】
(1)根据频率分布直方图,由每组的中间值乘以该组的频率,再求和,即可得出平均值;由中位数两侧频率之和均为![]() ,根据题中数据,即可求出结果;
,根据题中数据,即可求出结果;
(2)先由题意得,在这100件产品中,残次品有2件,设为![]() ,特优品有4件,设为
,特优品有4件,设为![]() ;用列举法,分别列举出“这6件产品中随机抽取2件”,“抽到2件残次品”,“抽到1件残次品”,“抽到2件特优品”对应的基本事件,基本事件个数比即为所求概率,比较概率大小,即可得出结果.
;用列举法,分别列举出“这6件产品中随机抽取2件”,“抽到2件残次品”,“抽到1件残次品”,“抽到2件特优品”对应的基本事件,基本事件个数比即为所求概率,比较概率大小,即可得出结果.
(1)由频率分布直方图可得估计平均数为:
![]() ;
;
设中位数为![]() ,则易知中位数
,则易知中位数![]() ,
,
所以![]() ,解得
,解得![]() ,
,
即产品的质量指标的中位数约为17.1.
(2)由频率分布直方图可知在这100件产品中,残次品有2件,设为![]() ,特优品有4件,设为
,特优品有4件,设为![]() .从这6件产品中随机抽取2件包含以下基本事件:
.从这6件产品中随机抽取2件包含以下基本事件:
![]()
![]() ,共15个基本事件.
,共15个基本事件.
若抽到2件残次品,该企业损失2万元,即收入为![]() 万元,该事件包含1个基本事件
万元,该事件包含1个基本事件![]() ,则概率为
,则概率为
![]()
若抽到1件残次品,1件特优品,该企业收入2万元,该事件包含8个基本事件:
![]()
则概率为![]() .
.
若抽到2件特优品,该企业收入6万元,其概率为![]()
综上可知,该企业收入2万元的可能性最大,为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(5分)《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第五节的容积为( )
A. 1升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点M(0,-1),直线l经过点N(2,1)且与椭圆C相交于A,B两点(异于点M),记直线MA的斜率为![]() ,直线MB的斜率为
,直线MB的斜率为![]() ,证明
,证明![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有微机![]() 台,分别放在
台,分别放在![]() 个房间,各房间开门钥匙互不相同.某期培训班有学员
个房间,各房间开门钥匙互不相同.某期培训班有学员![]() 人(
人(![]() ),每晚恰有
),每晚恰有![]() 人进机房实习操作,为保证每人一台机,至少应准备多少把钥匙分给这
人进机房实习操作,为保证每人一台机,至少应准备多少把钥匙分给这![]() 个学员,使得每晚不论哪
个学员,使得每晚不论哪![]() 个人进机房,都能用自己分到的钥匙打开一间机房的门进去练习,并按分得钥匙少的人先开门的原则,能保证每人恰可得到一个房间.
个人进机房,都能用自己分到的钥匙打开一间机房的门进去练习,并按分得钥匙少的人先开门的原则,能保证每人恰可得到一个房间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,BC∥AD,AB⊥BC,∠ADC=45°,PA⊥平面ABCD,AB=AP=1,AD=3.
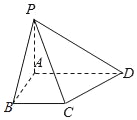
(1)求异面直线PB与CD所成角的大小;
(2)求点D到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图像如图所示,将
的部分图像如图所示,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
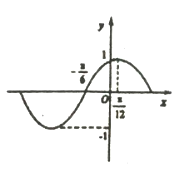
(1)求函数![]() 的解折式;
的解折式;
(2)在![]() 中,角
中,角![]() 满足
满足![]() ,且其外接圆的半径
,且其外接圆的半径![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com