练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

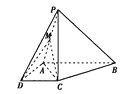
    【题目】如图，在四棱锥中， 平面.

    （1）求证： 平面；

    （2）若为线段的中点，且过三点平面与线段交于点，确定的位置，说明理由；

    并求三棱锥的高.

    【答案】(1)证明见解析；(2)答案见解析 .

    【解析】试题分析：

    (1)由题意可证得， ，则平面.

    (2) 为的中点，由几何关系可知：点为过三点的平面与线段的交点，结合棱锥的体积公式可得三棱锥的高为.

    试题解析：

    （1）在直角梯形中， ，

    ，所以，即，

    又平面，所以，又，故平面.

    （2）为的中点，

    因为为的中点， 为的中点，所以，且，

    又，所以，所以四点共面，

    所以点为过三点的平面与线段的交点，

    因为平面， 为的中点，所以到平面的距离，

    又，所以，

    有题意可知，在直角三角形中， ，

    在直角三角形中， ，所以.

    设三棱锥的高为，解得，

    故三棱锥的高为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=loga（1+x），g（x）=loga（1﹣x），其中a＞0且a≠1，设h（x）=f（x）﹣g（x）
    （1）求函数h（x）的定义域，判断h（x）的奇偶性并说明理由
    （2）解不等式h（x）＞0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ex﹣ax，（e为自然对数的底数）． （Ⅰ）讨论f（x）的单调性；
    （Ⅱ）若对任意实数x恒有f（x）≥0，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|y= }，B={x|x＜﹣4或x＞2}
    （1）若m=﹣2，求A∩（RB）；
    （2）若A∪B=B，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，P，Q分别是AA1 ， B1C1上的点，且AP=3A1P，B1C1=4B1Q．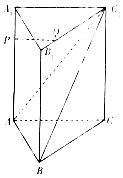
    （1）求证：PQ∥平面ABC1；
    （2）若AB=AA1 ， BC=3，AC1=3，BC1= ，求证：平面ABC1⊥平面AA1C1C．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PC⊥底面ABCD，ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2．E是PB的中点． （Ⅰ）求证：平面EAC⊥平面PBC；
    （Ⅱ）若二面角P﹣AC﹣E的余弦值为 ，求直线PA与平面EAC所成角的正弦值．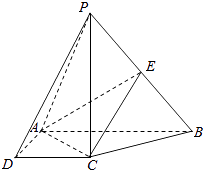

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2cos2ωx+2sinωxcosωx（ω＞0）的最小正周期为π．
    （1）求f（ ）的值；
    （2）求函数f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在棱长为6的正方体ABCD﹣A1B1C1D1中，M是BC的中点，点P是面DCC1D1内的动点，且满足∠APD=∠MPC，则三棱锥P﹣BCD的体积最大值是（ ）
    A.36
    B.12
    C.24
    D.18

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】底面是正多边形，顶点在底面的射影是底面中心的棱锥叫正棱锥．已知同底的两个正三棱锥内接于同一个球．已知两个正三棱锥的底面边长为a，球的半径为R．设两个正三棱锥的侧面与底面所成的角分别为α、β，则tan（α+β）的值是 ．

    查看答案和解析>>

    同步练习册答案