
【题目】定义在R上的偶函数f(x),且对任意实数x都有f(x+2)=f(x),当x∈[0,1]时,f(x)=x2,若在区间[﹣3,3]内,函数g(x)=f(x)﹣kx﹣3k有6个零点,则实数k的取值范围为__.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下列四种说法中正确的有______.(填序号)①数据2,2,3,3,4,6,7,3的众数与中位数相等;②数据1,3,5,7,9的方差是数据2,6,10,14,18的方差的一半;③一组数据的方差大小反映该组数据的波动性,若方差越大,则波动性越大,方差越小,则波动性越小.④频率分布直方图中各小长方形的面积等于相应各组的频数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】顺次连接椭圆![]() 的四个顶点恰好构成了一个边长为
的四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形。
的菱形。
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点,若直线
上的两个不同点,若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() (以
(以![]() 为坐标原点),线段
为坐标原点),线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接并延长交椭圆
,连接并延长交椭圆![]() 于点
于点![]() ,求椭圆
,求椭圆![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,教育部发文确定新高考改革正式启动,湖南、广东、湖北等8省市开始实行新高考制度,从2018年下学期的高一年级学生开始实行.为了适应新高考改革,某校组织了一次新高考质量测评,在成绩统计分析中,高二某班的数学成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
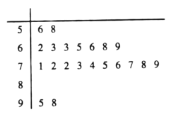
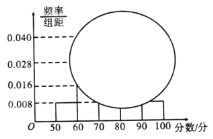
(1)求该班数学成绩在![]() 的频率及全班人数;
的频率及全班人数;
(2)根据频率分布直方图估计该班这次测评的数学平均分;
(3)若规定![]() 分及其以上为优秀,现从该班分数在
分及其以上为优秀,现从该班分数在![]() 分及其以上的试卷中任取
分及其以上的试卷中任取![]() 份分析学生得分情况,求在抽取的
份分析学生得分情况,求在抽取的![]() 份试卷中至少有
份试卷中至少有![]() 份优秀的概率.
份优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an} 满足a1=a,![]() =can+1﹣c(n∈N*),其中a、c为实数,且c≠0.
=can+1﹣c(n∈N*),其中a、c为实数,且c≠0.
(1)求数列{an} 的通项公式;
(2)设a=![]() ,c=
,c=![]() ,bn=n(1﹣an)(n∈N*),求数列 {bn}的前n项和Sn.
,bn=n(1﹣an)(n∈N*),求数列 {bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,点
,点![]() 是椭圆上的一个动点,
是椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)已知点![]() ,问是否存在直线
,问是否存在直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,若存在,求出直线
,若存在,求出直线![]() 斜率的取值范围;若不存在,说明理由.
斜率的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( ).
①“若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于2”的逆命题是真命题;
中至少有一个不小于2”的逆命题是真命题;
②命题“设![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是一个真命题;
”是一个真命题;
③命题![]() ,
,![]() ,则
,则![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
④命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”.
”.
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的长轴长为4,左、右顶点分别为
的长轴长为4,左、右顶点分别为![]() ,经过点
,经过点![]() 的动直线与椭圆
的动直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() (不与点
(不与点![]() 重合).
重合).
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)求四边形![]() 面积的最大值;
面积的最大值;
(3)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,判断点
,判断点![]() 是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com