
分析 (1)根据题意,分析可得点M到点F(1,0)的距离与其到直线x=1的距离相等,进而分析可得点M的轨迹为抛物线,且其焦点为F(1,0),准线为x=-1,由抛物线的标准方程计算可得答案;
(2)①联立直线x=my+1与抛物线的方程,可得y2-4my-4=0,利用韦达定理,可得结论;
②设D(-1,y2),则kAO-kOD=$\frac{{y}_{1}}{{x}_{1}}-{y}_{2}$=$\frac{4+{y}_{1}{y}_{2}}{{y}_{1}}$=0,即可证明结论.
解答 解:(1)根据题意,点M到点F(1,0)的距离比它到直线x=-3的距离小1,
即点M到点F(1,0)的距离与其到直线x=-1的距离相等,
则点M的轨迹为抛物线,且其焦点为F(1,0),准线为x=-1,
则其轨迹方程为y2=4x; …(6分)
(2)①联立直线x=my+1与抛物线的方程,可得y2-4my-4=0,
∴y1•y2=-4,x1•x2=1 …(9分)
②设D(-1,y2),则kAO-kOD=$\frac{{y}_{1}}{{x}_{1}}-{y}_{2}$=$\frac{4+{y}_{1}{y}_{2}}{{y}_{1}}$=0,
所以A、O、D三点共线.…(12分)
点评 本题考查抛物线的定义以及抛物线的标准方程,考查直线与抛物线的位置关系,关键是灵活运用抛物线的定义.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2) | B. | (1,2) | C. | $[{1,\frac{3}{2}})$ | D. | $({1,\frac{3}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
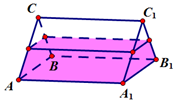 如图,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点,当底面ABC水平放置时,液面高为( )
如图,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点,当底面ABC水平放置时,液面高为( )| A. | 7 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分条件又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$) | B. | [$\frac{1}{4}$,1) | C. | ($\frac{1}{16}$,1) | D. | [$\frac{1}{16}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
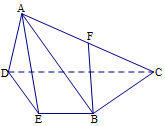 如图,在空间几何体A-BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点.
如图,在空间几何体A-BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com