
分析 (1)根据向量数量积的坐标表示及辅助角公式,即可求得f(x)的解析式,由正弦函数性质即可求得f(x)的值域;
(2)当x=$\frac{π}{3}$,代入求得$\overrightarrow{a}$,根据向量的坐标运算分别求得2$\overrightarrow{a}$-$\overrightarrow{b}$与$λ\overrightarrow{a}$+$\overrightarrow{b}$,利用向量垂直的定义,代入即可求得λ的值.
解答 解:(1)f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{\sqrt{3}}{3}$sinx×3+2cosx×(-$\frac{1}{2}$)
=$\sqrt{3}$sinx-cosx,
=2sin(x-$\frac{π}{6}$),
由正弦函数的性质可知:-1≤sin(x-$\frac{π}{6}$)≤1,
∴-2≤sin(x-$\frac{π}{6}$)≤2,
f(x)的值域[-2,2];
(2)当x=$\frac{π}{3}$,$\overrightarrow{a}$=($\frac{1}{2}$,1),
∴2$\overrightarrow{a}$-$\overrightarrow{b}$=(-2,$\frac{5}{2}$)
$λ\overrightarrow{a}$+$\overrightarrow{b}$=($\frac{λ+6}{2}$,$\frac{2λ-1}{2}$),
∵(2$\overrightarrow{a}$-$\overrightarrow{b}$)⊥($λ\overrightarrow{a}$+$\overrightarrow{b}$),
∴(2$\overrightarrow{a}$-$\overrightarrow{b}$)•($λ\overrightarrow{a}$+$\overrightarrow{b}$)=0,
$\frac{λ+6}{2}$×(-2)+$\frac{2λ-1}{2}$×$\frac{5}{2}$=0,
解得:λ=$\frac{29}{6}$,
λ的值$\frac{29}{6}$.
点评 本题考查向量数量积的坐标运算,三角恒等变换,向量垂直的定义,考查综合分析问题及解决问题的能力,属于中档题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
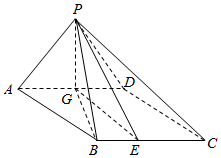 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,$\frac{1}{3}$] | B. | [-1,1] | C. | [-$\frac{1}{3}$,+∞) | D. | [-$\frac{4}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 评分等级 | [0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
| 男(人数) | 2 | 5 | 9 | 5 | 4 |
| 女(人数) | 1 | 2 | 5 | 10 | 7 |
| 满意 | 不满意 | 总计 | |
| 男 | 16 | 9 | 25 |
| 女 | 8 | 17 | 25 |
| 总计 | 24 | 26 | 50 |
| P=(K2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 等腰梯形ABCD中,AD∥BC,AC、BD交于点Q,AC平分∠DAB,AP为梯形ABCD外接圆的切线,交BD的延长线于点P.
等腰梯形ABCD中,AD∥BC,AC、BD交于点Q,AC平分∠DAB,AP为梯形ABCD外接圆的切线,交BD的延长线于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com