
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足① ![]() ;② 当
;② 当![]() ,且
,且![]() 时,都有
时,都有![]() ;③ 当
;③ 当![]() ,且
,且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:①
为“偏对称函数”.现给出四个函数:①![]() ;②
;② ![]() ; ③
; ③![]() ;④
;④![]() .则其中是“偏对称函数”的函数序号为 _______.
.则其中是“偏对称函数”的函数序号为 _______.
【答案】①④.
【解析】分析:条件②等价于f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增,条件③等价于f(x)﹣f(﹣x)<0在(﹣∞,0)上恒成立,依次判断各函数是否满足条件即可得出结论.
详解:由②可知当x>0时,f′(x)>0,当x<0时,f′(x)<0,
∴f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增,
f2(x)=ln(![]() ﹣x)=ln
﹣x)=ln![]() ,∴f2(x)在R上单调递减,不满足条件②,
,∴f2(x)在R上单调递减,不满足条件②,
∴f2(x)不是“偏对称函数”;
又![]() (
(![]() )=
)=![]() (
(![]() )=0,∴
)=0,∴![]() (x)在(0,+∞)上不单调,故
(x)在(0,+∞)上不单调,故![]() (x)不满足条件②,
(x)不满足条件②,
∴![]() (x)不是“偏对称函数”;
(x)不是“偏对称函数”;
又f2(x)=ln(![]() ﹣x)=ln
﹣x)=ln![]() ,∴f2(x)在R上单调递减,不满足条件②,
,∴f2(x)在R上单调递减,不满足条件②,
∴f2(x)不是“偏对称函数”;
由③可知当x1<0时,f(x1)<f(﹣x2),即f(x)﹣f(﹣x)<0在(﹣∞,0)上恒成立,
对于![]() (x),当x<0时,
(x),当x<0时,![]() (x)﹣
(x)﹣![]() (﹣x)=﹣x﹣e﹣x+1,
(﹣x)=﹣x﹣e﹣x+1,
令h(x)=﹣x﹣e﹣x+1,则h′(x)=﹣1+e﹣x>0,
∴h(x)在(﹣∞,0)上单调递增,故h(x)<h(0)=0,满足条件③,
由基本初等函数的性质可知![]() (x)满足条件①,②,
(x)满足条件①,②,
∴![]() (x)为“偏对称函数”;
(x)为“偏对称函数”;
对于f4(x),f4′(x)=2e2x﹣ex﹣1=2(ex﹣![]() )2﹣
)2﹣![]() ,
,
∴当x<0时,0<ex<1,∴f4′(x)<2(1﹣![]() )2﹣
)2﹣![]() =0,
=0,
当x>0时,ex>1,∴f4′(x)>2(1﹣![]() )2﹣
)2﹣![]() =0,
=0,
∴f4(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增,满足条件②,
当x<0,令m(x)=f4(x)﹣f4(﹣x)=e2x﹣e﹣2x+e﹣x﹣ex﹣2x,
则m′(x)=2e2x+2e﹣2x﹣e﹣x﹣ex﹣2=2(e2x+e﹣2x)﹣(e﹣x+ex)﹣2,
令e﹣x+ex=t,则t≥2,于是m′(x)=2t2﹣t﹣6=2(t﹣![]() )2﹣
)2﹣![]() ≥2(2﹣
≥2(2﹣![]() )2﹣
)2﹣![]() =0,
=0,
∴m(x)在(﹣∞,0)上单调递增,
∴m(x)<m(0)=0,故f4(x)满足条件③,
又f4(0)=0,即f4(x)满足条件①,
∴f4(x)为“偏对称函数”.
故答案为:①④.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】在某市高三教学质量检测中,全市共有![]() 名学生参加了本次考试,其中示范性高中参加考试学生人数为
名学生参加了本次考试,其中示范性高中参加考试学生人数为![]() 人,非示范性高中参加考试学生人数为
人,非示范性高中参加考试学生人数为![]() 人.现从所有参加考试的学生中随机抽取
人.现从所有参加考试的学生中随机抽取![]() 人,作检测成绩数据分析.
人,作检测成绩数据分析.

(1)设计合理的抽样方案(说明抽样方法和样本构成即可);
(2)依据![]() 人的数学成绩绘制了如图所示的频率分布直方图,据此估计本次检测全市学生数学成绩的平均分;
人的数学成绩绘制了如图所示的频率分布直方图,据此估计本次检测全市学生数学成绩的平均分;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE= ![]() BC,PB⊥AE.
BC,PB⊥AE. 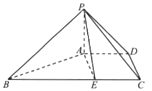
(1)求证:AB⊥PE;
(2)求二面角B﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中,不可能成立的是( )
,下列选项中,不可能成立的是( )
A. ![]() 没有最大元素,
没有最大元素, ![]() 有一个最小元素 B.
有一个最小元素 B. ![]() 没有最大元素,
没有最大元素, ![]() 也没有最小元素
也没有最小元素
C. ![]() 有一个最大元素,
有一个最大元素, ![]() 有一个最小元素 D.
有一个最小元素 D. ![]() 有一个最大元素,
有一个最大元素, ![]() 没有最小元素
没有最小元素
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)过点M(m,2),其焦点为F,且|MF|=2.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设E为y轴上异于原点的任意一点,过点E作不经过原点的两条直线分别与抛物线C和圆F:(x﹣1)2+y2=1相切,切点分别为A,B,求证:直线AB过定点F(1,0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“?x∈R,2x>0”的否定是“?x0∈R,2 ![]() <0”
<0”
B.命题“若sinx=siny,则x=y”的逆否命题为真命题
C.若命题p,¬q都是真命题,则命题“p∧q”为真命题
D.命题“若△ABC为锐角三角形,则有sinA>cosB”是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com