【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，直线
的方程为
，曲线
：
（
为参数，
），在以原点
为极点，
轴正半轴为极轴的极坐标系中，曲线
：
.
（1）求曲线的普通方程和曲线的直角坐标方程；
（2）若直线与曲线有公共点，且直线与曲线的交点
恰好在曲线与轴围成的区域（不含边界）内，求
的取值范围.
科目：高中数学 来源： 题型：
【题目】浙江省现行的高考招生制度规定除语、数、英之外，考生须从政治、历史、地理、物理、化学、生物、技术这7门高中学考科目中选择3门作为高考选考科目，成绩计入高考总分.已知报考某高校
、
两个专业各需要一门科目满足要求即可，专业：物理、化学、技术；专业：历史、地理、技术.考生小李今年打算报考该高校这两个专业的选考方式有______ 种.（用数字作答）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知A,B两点都在以PC为直径的球O的表面上，AB⊥BC，AB=2，BC=4，若球O的体积为
，则三棱锥P-ABC表面积为___________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=x3+bx2+cx（x∈R），已知g（x）=f（x）﹣f′（x）是奇函数
（1）求b、c的值．
（2）求g（x）的单调区间与极值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某医药公司研发一种新的保健产品，从生产的一批产品中抽取200盒作为样本，测量产品的一项质量指标值，该指标值越高越好.由测量结果得到如下频率分布直方图：
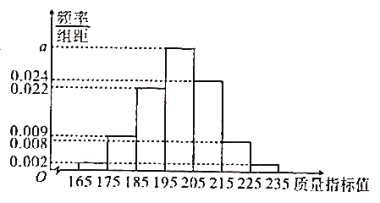
（Ⅰ）求
，并试估计这200盒产品的该项指标的平均值；
（Ⅱ）国家有关部门规定每盒产品该项指标值不低于150均为合格，且按指标值的从低到高依次分为：合格、优良、优秀三个等级，其中
为优良，不高于185为合格，不低于215为优秀.用样本的该项质量指标值的频率代替产品的该项质量指标值的概率.
①求产品该项指标值的优秀率；
②现从这批产品中随机抽取3盒，求其中至少有1盒该项质量指标值为优秀的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，已知动直线
的参数方程：
，（
为参数，
） ，以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（Ⅰ）求曲线的直角坐标方程；
（Ⅱ）若直线与曲线恰好有2个公共点时，求直线的一般方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】中国改革开放以来经济发展迅猛，某一线城市的城镇居民2012～2018年人均可支配月收入散点图如下（年份均用末位数字减1表示）.
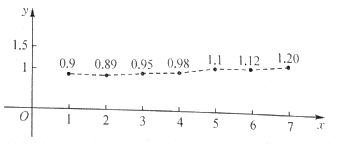
（1）由散点图可知，人均可支配月收入y（万元）与年份x之间具有较强的线性相关关系，试求y关于x的回归方程（系数精确到0.001），依此相关关系预测2019年该城市人均可支配月收入；
（2）在2014～2018年的五个年份中随机抽取两个数据作样本分析，求所取的两个数据中，人均可支配月收入恰好有一个超过1万元的概率.
注：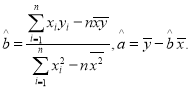
，
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为比较甲、乙两名蓝球运动员的近期竞技状态，选取这两名球员最近五场比赛的得分制成如图所示的茎叶图，有下列结论：
甲 | 乙 | |||||
9 | 8 | 5 | 2 | 8 | 9 | |
2 | 1 | 3 | 0 | 1 | 2 |
①甲最近五场比赛得分的中位数高于乙最近五场比赛得分的中位数.
②甲最近五场比赛得分的平均数低于乙最近五场比赛得分的平均数.
③从最近五场比赛的得分看，乙比甲更稳定.
④从最近五场比赛的得分看，甲比乙更稳定.
其中所有正确结论的编号为（ ）
A.①③B.①④C.②③D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
