
【题目】设![]() 为实数,
为实数,![]() .
.
(1)证明:不论![]() 为何实数,f(x)均为增函数;
为何实数,f(x)均为增函数;
(2)试确定![]() 的值,使f(-x)+ f(x)=0成立.
的值,使f(-x)+ f(x)=0成立.
【答案】(1)证明见解析(2)1
【解析】
(1)任取x1<x2,判断f(x1)﹣f(x2)的符号,进而根据函数单调性的定义,可得结论;
(2)若f(﹣x)+f(x)=0恒成立,则f(x)为奇函数,由奇函数的性质有 f(0)=0,代入可求a,则f(x)为奇函数,由奇函数的性质有 f(0)=0,代入可求a.
证明:(1)设存在任意x1<x2,
∴![]() ,
,![]() ,
,![]() ,
,
则f(x1)﹣f(x2)![]() (
(![]() )
)![]()
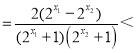 0,
0,
∴f(x1)<f(x2),
∴不论a为何实数,f(x)均为增函数.
解:(2)若f(﹣x)+f(x)=0,则f(x)为奇函数,
则f(0)=a﹣1=0,
∴a=1,
当a=1时,f(x)=1![]() 满足f(﹣x)+f(x)=0恒成立.
满足f(﹣x)+f(x)=0恒成立.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】(Ⅰ)求过点A(2,6)且在两坐标轴上的截距相等的直线m的方程;
(Ⅱ)求过点A(2,6)且被圆C:(x﹣3)2+(y﹣4)2=4截得的弦长为![]() 的直线l的方程.
的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.

(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
附: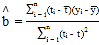 ,
,![]() . 参考数据:
. 参考数据: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为备战2016年奥运会,甲、乙两位射击选手进行了强化训练.现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次,记录如下:
甲:8.3,9.0,7.9,7.8,9.4,8.9,8.4,8.3
乙:9.2,9.5,8.0,7.5,8.2,8.1,9.0,8.5
(1)画出甲、乙两位选手成绩的茎叶图;
(2)现要从中选派一人参加奥运会封闭集训,从统计学角度,你认为派哪位选手参加合理?简单说明理由;
(3)若将频率视为概率,对选手乙在今后的三次比赛成绩进行预测,记这三次成绩中不低于8.5分的次数为ξ,求ξ的分布列及均值E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:![]() .
.
(1)求圆的圆心C的坐标和半径长;
(2)直线l经过坐标原点且不与y轴重合,l与圆C相交于![]() 两点,求证:
两点,求证:![]() 为定值;
为定值;
(3)斜率为1的直线m与圆C相交于D、E两点,求直线m的方程,使![]() 的面积最大.
的面积最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com