
����Ŀ��������12�֣�ѧϰ�澫��ǰ������ij��λ�����Ĺ̶����ξ�������ѧϰ�澫��ʱȫ�ã���λ��ѧϰ�澫��ǰ��������ڲ��ε����������һ������ͳ�ƣ������������£�
������ | ����� | �� �� | |
ѧϰ�澫��ǰ | 50 | 150 | 200 |
ѧϰ�澫��� | 30 | 170 | 200 |
�� �� | 80 | 320 | 400 |
��������:ѧϰ�澫��ǰ������İٷֱȷֱ��Ƕ���?�������ж���ٲ���������ѧϰ�澫���Ƿ��йأ�
��������˵���Ƿ���97��5%���ϵİ�����Ϊ��ٲ���������ѧϰ�澫���йأ�
�ο���ʽ��![]() ��
��![]()
P��K2��k0�� | 0��05 | 0��025 | 0��010 | 0��005 | 0��001 |
k0 | 3��841 | 5��024 | 6��635 | 7��879 | 10��828 |
���𰸡�������![]() ;��������
;��������![]() ���ϵİ�����Ϊ��ٲ���������ѧϰ�澫���йأ�
���ϵİ�����Ϊ��ٲ���������ѧϰ�澫���йأ�
�������������������1�� ѧϰ�澫��ǰ�����ε��İٷֱȷֱ���:![]() ,
,![]() �����������ٷֱȲ�����ԣ��ʳ����ж�������μ�����ѧϰ�澫���Ƿ��йأ���2�����ݶ�ѧϰ�澫��ǰ��������ڲ��ε���������������������
�����������ٷֱȲ�����ԣ��ʳ����ж�������μ�����ѧϰ�澫���Ƿ��йأ���2�����ݶ�ѧϰ�澫��ǰ��������ڲ��ε���������������������![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() ��ֵΪ
��ֵΪ![]() ���ٸ���
���ٸ���![]() ,��У����ѧ������ٲ���������ѧϰ�澫�����й�.
,��У����ѧ������ٲ���������ѧϰ�澫�����й�.
���������
�⣺��1�� ѧϰ�澫��ǰ���ε��İٷֱ���:![]()
ѧϰ�澫������ε��İٷֱ���:![]() ��
��
��Ϊ���������ԵIJ���,���Գ����ж�������μ�����ѧϰ�澫���Ƿ��й�.
��2���������е����ݼ��㣺![]()
��Ϊ![]() ��������97.5%�İ�����Ϊ���������������ѧϰ�澫���йء�
��������97.5%�İ�����Ϊ���������������ѧϰ�澫���йء�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ƽ�������ABCDE�У�AB��CD����BAD=90�㣬AB=2��CD=1����ADE�DZ߳�Ϊ2���������Σ��ֽ���ADE��AD���𣬵õ�����E��ABCD����ͼ2������DE��AB��
������֤��ƽ��ADE��ƽ��ABCD��
������ƽ��BCE��ƽ��ADE���������ǵĴ�С��
��������AE���Ƿ���ڵ�F��ʹ��DF��ƽ��BCE�������ڣ��� ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�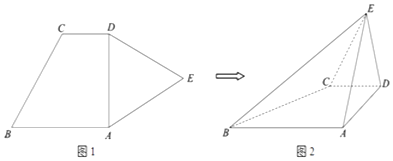
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽ⴺ����ҹ�²��С��ij���ӷ�ѿ����֮��Ĺ�ϵ�����ڴ�4�·ݵ�30���������ѡ��5������о����ҷֱ��¼��ÿ����ҹ�²���ÿ��ÿ100�����ӽ��ݺ�ķ�ѿ�����õ����±���
���� | 4��1�� | 4��7�� | 4��15�� | 4��21�� | 4��30�� |
�²�x/�� | 10 | 11 | 13 | 12 | 8 |
��ѿ��y/�� | 23 | 25 | 30 | 26 | 16 |
��1������5������ѡ2��,�Ƿ�ѿ���������ֱ�Ϊ![]() ,���¼���
,���¼���![]() ����С��25���ĸ��ʣ�
����С��25���ĸ��ʣ�
��2�� �������Իع鷽�̵õ��Ĺ���������4�·���ѡ5��ļ������ݵ�����������2�ţ�����Ϊ�õ������Իع鷽���ǿɿ���. �����4��7����4��15����4��21������������ݣ����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() �����ж����õ����Իع鷽���Ƿ�ɿ���
�����ж����õ����Իع鷽���Ƿ�ɿ���
�ο���ʽ:  ��
�� ![]()
�����: ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��A1B1C1D1�У�E��F�ֱ�Ϊ��DD1��BC�е�GΪ��A1B1������һ�㣬��ֱ��AE��ֱ��FG���ɵĽ�Ϊ�� �� 
A.30��
B.45��
C.60��
D.90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ı���ABCD��AC��BD��CE=2AE=2BE=2DE=2�����ı���ABCD����BD�۵����õ�ͼ2��ʾ������A��BCD������AB��CD�� 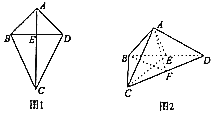
��1��֤����ƽ��ACD��ƽ��BAD��
��2����FΪCD�е㣬������C��AB��F������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=xln��x��1����a��x��2����
������a=2017��������f��x����x=2�������߷��̣�
��������x��2ʱ��f��x����0����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����Ϊ����������![]() ������
������![]() ��
�� ![]() ������
������![]() ��ǰ
��ǰ![]() ��ͣ������㣺
��ͣ������㣺
![]() .
.
��1����![]() �ɵȱ����У���ʵ��
�ɵȱ����У���ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ����֤������
����֤������ Ϊ�Ȳ����У�
Ϊ�Ȳ����У�
��3���ڣ�2���������£���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B��C����ABC�������ڽǣ��������и������У�����ȷ��Ϊ( ��)
A. sin2A��sin2B��sin2C��2sinBsinCcos(B��C)
B. sin2B��sin2A��sin2C��2sinAsinCcos(A��C)
C. sin2C��sin2A��sin2B-2sinAsinBcosC
D. sin2(A��B)��sin2A��sin2B-2sinBsinCcos(A��B)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() =
= ![]()
(1)����![]() �ĵ�����������;
�ĵ�����������;
(2)��ABC�ڽ�A,B,C�ĶԱ߷ֱ�Ϊa,b,c,��![]() =
=![]() ,b=1,
,b=1, ![]() =
=![]() ,��a
,��a![]() b,�����B�ͽ�
b,�����B�ͽ�![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com