
【题目】已知![]() ,
,![]() 为实数,函数
为实数,函数![]() ,且函数
,且函数![]() 是偶函数,函数
是偶函数,函数![]() 在区间
在区间![]() 上是减函数,且在区间
上是减函数,且在区间![]() 上是增函数.
上是增函数.
(1)求函数![]() 的解析式;
的解析式;
(2)求实数![]() 的值;
的值;
(3)设![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 在区间
在区间![]() 上有最小值-2?若存在,求出
上有最小值-2?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]()
【解析】
(1)利用函数![]() 是偶函数,求函数
是偶函数,求函数![]() 的解析式;
的解析式;
(2)利用复合函数的单调性,求实数b的值;
(3)分类讨论,求出函数的最小值,利用![]() 在区间
在区间![]() 上有最小值为﹣2,得出结论.
上有最小值为﹣2,得出结论.
(1)∵函数![]() 是偶函数,∴(x+1)2+a(x+1)+1=(﹣x+1)2+a(﹣x+1)+1,∴4x+2ax=0,∴a=﹣2,
是偶函数,∴(x+1)2+a(x+1)+1=(﹣x+1)2+a(﹣x+1)+1,∴4x+2ax=0,∴a=﹣2,
∴![]() =(x﹣1)2;
=(x﹣1)2;
(2)![]() =﹣bx4+(5b﹣1)x2+2﹣b,
=﹣bx4+(5b﹣1)x2+2﹣b,
令t=x2,u(t)=﹣bt2+(5b﹣1)t﹣(b﹣2),
在区间![]() 上,t=x2是减函数,且t∈
上,t=x2是减函数,且t∈![]() ,由
,由![]() 是减函数,可知
是减函数,可知![]() 为增函数;
为增函数;
在区间![]() 上,t=x2是减函数,且t∈(0,4),由
上,t=x2是减函数,且t∈(0,4),由![]() 是增函数,可知
是增函数,可知![]() 为减函数,
为减函数,
∴由![]() 在(0,4)上是减函数,(4,+∞)上是增函数,可得二次函数开口向上,b<0,且﹣
在(0,4)上是减函数,(4,+∞)上是增函数,可得二次函数开口向上,b<0,且﹣![]() =4,
=4,
∴![]() ;
;
(3)![]() ,x∈[0,2].
,x∈[0,2].
当q<0,ymin=h(0)=1+2q=﹣2,q=﹣![]() ;
;
当0≤q≤2,ymin=h(q)=﹣q2+2q+1=﹣2,∴q=3或﹣1,舍去;
当q>2,ymin=h(2)=﹣2q+5=﹣2,q=![]() ,
,
综上所述:![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的通项公式为
的通项公式为![]() ,其中
,其中![]() ,
,![]() 、
、![]() .
.
(1)试写出一组![]() 、
、![]() 的值,使得数列
的值,使得数列![]() 中的各项均为正数.
中的各项均为正数.
(2)若![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,且对任意的
,且对任意的![]() (
(![]() ),均有
),均有![]() ,写出所有满足条件的
,写出所有满足条件的![]() 的值.
的值.
(3)若![]() ,数列
,数列![]() 满足
满足![]() ,其前
,其前![]() 项和为
项和为![]() ,且使
,且使![]() (
(![]() 、
、![]() ,
,![]() )的
)的![]() 和
和![]() 有且仅有
有且仅有![]() 组,
组,![]() 、
、![]() 、…、
、…、![]() 中有至少
中有至少![]() 个连续项的值相等,其它项的值均不相等,求
个连续项的值相等,其它项的值均不相等,求![]() 、
、![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式为 an=(n﹣k1)(n﹣k2),其中k1,k2∈Z:
(1)试写出一组k1,k2∈Z的值,使得数列{an}中的各项均为正数;
(2)若k1=1、k2∈N*,数列{bn}满足bn=![]() ,且对任意m∈N*(m≠3),均有b3<bm,写出所有满足条件的k2的值;
,且对任意m∈N*(m≠3),均有b3<bm,写出所有满足条件的k2的值;
(3)若0<k1<k2,数列{cn}满足cn=an+|an|,其前n项和为Sn,且使ci=cj≠0(i,j∈N*,i<j)的i和j有且仅有4组,S1、S2、…、Sn中至少3个连续项的值相等,其他项的值均不相等,求k1,k2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个三角形数表按如下方式构成(如图:其中项数![]() ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:![]() ;
;![]() 为数表中第
为数表中第![]() 行的第
行的第![]() 个数.
个数.
![]()
![]() …
…![]()
![]()
![]()
![]() …
…![]()
![]() …
…![]()
……
![]()
(1)求第2行和第3行的通项公式![]() 和
和![]() ;
;
(2)证明:数表中除最后2行外每一行的数都依次成等差数列,并求![]() 关于
关于![]() 的表达式;
的表达式;
(3)若![]() ,
,![]() ,试求一个等比数列
,试求一个等比数列![]() ,使得
,使得![]() ,且对于任意的
,且对于任意的![]() ,均存在实数
,均存在实数![]() ,当
,当![]() 时,都有
时,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1的侧面AA1B1B是菱形,侧面AA1C1C是矩形,平面AA1C1C⊥平面AA1B1B,∠BAA1![]() ,AA1=2AC=2,O为AA1的中点.
,AA1=2AC=2,O为AA1的中点.
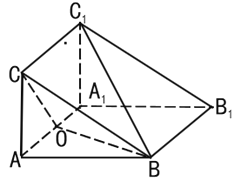
(1)求证:OC⊥BC1;
(2)求点C1到平面ABC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)作出函数![]() 的图像;
的图像;
(2)根据(1)所得图像,填写下面的表格:
性质 | 定义域 | 值域 | 单调性 | 奇偶性 | 零点 |
|
(3)关于![]() 的方程
的方程![]() 恰有6个不同的实数解,求
恰有6个不同的实数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com